圖論應用題 驗證二元樹節點 Validate Binary Tree Nodes_Leetcode #1361

Todd Quackenbush on Unsplash

這題的題目在這裡:

題目敘述

題目會給我們節點總數目n、左子樹的關係陣列、右子樹的關係陣列，要求我們驗證在給定的條件下，能不能構成一顆合法的二元樹。

測試範例

Example 1: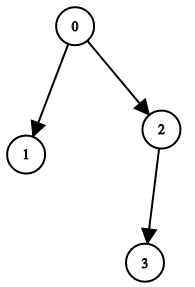

Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,-1,-1,-1]
Output: true

Example 2:

Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,3,-1,-1]
Output: false

Example 3:

Input: n = 2, leftChild = [1,0], rightChild = [-1,-1]
Output: false

約束條件

Constraints:

• n == leftChild.length == rightChild.length
• 1 <= n <= 104
• -1 <= leftChild[i], rightChild[i] <= n - 1

演算法

先找出根結點，根結點Root不會是別人的子樹，所以根結點Root一定不會出現在leftChild和RightChild這兩個關係陣列。

如果根結點Root找不到，代表樹根不存在，樹根不存在可以提早返回False，代表這不是一顆合法的二元樹。

如果根結點找的到，那接下來就用經典的DFS或者BFS，以根結點Root為起始點，拜訪整顆二元樹。

假如最後剛好拜訪n個節點，並且沒有重複，那麼就可以驗證這是一顆合法的二元樹。

如果有重複拜訪，代表途中存在環路，二元樹不允許環路Cycle出現，直接返回False，代表這不是一顆合法的二元樹。

程式碼

class Solution:
　def validateBinaryTreeNodes(self, n: int, leftChild: List[int], rightChild: List[int]) -> bool:
　　
　　# Definition of NULL (i.e., empty node), given by description
　　NULL = -1
　　
　　# --------------------------------------------------------------
　　def find_root():
　　　
　　　children = set(leftChild) | set(rightChild)

　　　# search for root node, root node is not a child node always.
　　　for i in range(n):
　　　　if i not in children:
　　　　　return i
　　　
　　　return NULL
　　
　　# --------------------------------------------------------------
　　
　　root = find_root()
　　
　　if root == NULL:
　　　# Reject, because root doesn't exist
　　　return False
　　
　　
　　
　　# launch BFS to given graph
　　queue = deque([root])
　　visited = set()
　　
　　while queue:
　　　
　　　cur = queue.popleft()
　　　
　　　if cur in visited:
　　　　
　　　　# Reject, because there is a cycle
　　　　# Cycle is not allowed in binary tree
　　　　return False
　　　
　　　visited.add(cur)
　　　
　　　if leftChild[cur] != NULL:
　　　　queue.append( leftChild[cur] )
　　　　
　　　if rightChild[cur] != NULL:
　　　　queue.append( rightChild[cur] )
　　
　　
　　# BFS in binary tree must visit n nodes exactly, without repetition.
　　return len(visited) == n

複雜度分析

時間複雜度: O( n)
定位根結點耗費O(n)，拜訪整棵樹也耗費O(n)

空間複雜度: O(n)
演算法中，建立了一個children集合，所佔用記憶體空間為O(n)

BFS拜訪所用到的Queue或者DFS拜訪所用到的Stack，佔用空間最多也為O(n)

關鍵知識點

拜訪二元樹，就想到經典的DFS和者BFS模板。

另外，二元樹裡面，不允許環路Cycle出現。

Reference:

[1] Python O(n) by DFS / BFS / UnionFind [w/ Comment] - Validate Binary Tree Nodes - LeetCode