
題目敘述
題目會給一顆二元樹,要求我們計算節點值 和 子樹平均值相等的node有幾個。
測試範例
Example 1: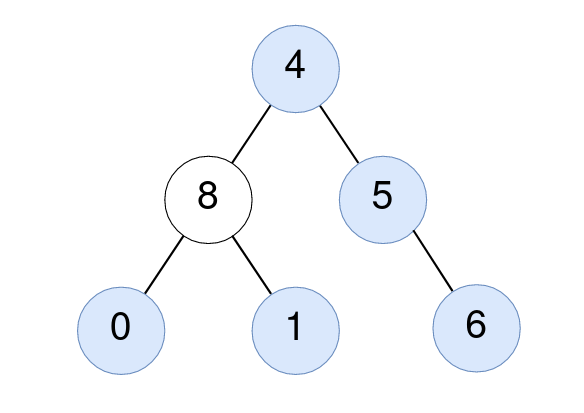
Input: root = [4,8,5,0,1,null,6]
Output: 5
Explanation:
For the node with value 4: The average of its subtree is (4 + 8 + 5 + 0 + 1 + 6) / 6 = 24 / 6 = 4.
For the node with value 5: The average of its subtree is (5 + 6) / 2 = 11 / 2 = 5.
For the node with value 0: The average of its subtree is 0 / 1 = 0.
For the node with value 1: The average of its subtree is 1 / 1 = 1.
For the node with value 6: The average of its subtree is 6 / 1 = 6.
Example 2:

Input: root = [1]
Output: 1
Explanation: For the node with value 1: The average of its subtree is 1 / 1 = 1.
約束條件
Constraints:
- The number of nodes in the tree is in the range
[1, 1000]. 0 <= Node.val <= 1000
演算法
抽象來想,對於當下節點來說,需要知道下列資訊來滿足題目要求的計算
- 子樹的結點值總和
- 子樹的valid count (就是子樹內部,節點值=子樹平均值的node count)
- 子樹的總結點數(因為平均 = 子樹結點值總和/子樹總結點數,我們會需要分子和分母的確切數值)
依循這個思路,設計DFS 遞迴function,以bottom-up 由下往上的方式,回傳 上述三個參數給parent node,逐層計算節點值 和 子樹平均值相等的node有幾個。
程式碼
class Solution:
def averageOfSubtree(self, root: Optional[TreeNode]) -> int:
def helper(root):
if not root:
# node value, valid count, total node count
return 0, 0, 0
l_sum, l_valid, l_nodes = helper(root.left)
r_sum, r_valid, r_nodes = helper(root.right)
# Average = (root + left subtree + right subtree) / subtree node count
avg = (root.val + l_sum + r_sum) // (1 + l_nodes + r_nodes )
if root.val == avg:
return l_sum + r_sum + root.val, l_valid + r_valid + 1, l_nodes + r_nodes + 1
else:
return l_sum + r_sum + root.val, l_valid + r_valid, l_nodes + r_nodes + 1
# ===========================
# Our goal is valid count
return helper(root)[1]
複雜度分析
時間複雜度:
O( n ) DFS 拜訪每個節點,每個節點拜訪一次。
空間複雜度:
O( n ) DFS 拜訪每個節點,最深深度為O(n),發生在整棵樹向左歪斜或向右歪斜時。
關鍵知識點
DFS function 傳統上都是回傳一個參數,或者直接return不帶回傳值。
這題的關鍵考點在於,我們需要的各種資訊都隱含在子樹裡,而且不只一個欄位。
接著想到,function其實可以return 多重欄位的回傳值,回傳給parent node 去計算題目所要求的目標值。
Reference:
[1] Python O(n) by DFS - Count Nodes Equal to Average of Subtree - LeetCode



















