🔼用Python來實現 Min Heap 最小堆

Markus Spiske on Unsplash

定義

Min-Heap 最小堆是一種特殊的樹狀資料結構，
其中每個節點的值都小於或等於其子節點的值。這意味著最小值總是位於根節點。

Min-Heap 常用於實作優先權佇列 (Priority Queue)、Dijkstra 演算法、
排序以及尋找中位數等應用。

優點

1.根節點永遠保持目前數據流的最小值。

2.如果依序pop n次，將得到一個從小到大排序好的序列。

3.可以override"最小"的定義，擴充為優先權佇列priority queue。

缺點

1.不支援直接取出第k小元素的操作, k > 1。

2.新增、刪除都需要動態調整的成本，來保持min heap最小堆的性質。

run-time成本 = O(log n)。

MinHeap的class定義 與 建構子

class MinHeap:
  def __init__(self):
  	
  	# 初始化時，是一個空的堆積empty heap
    self.heap = []

MinHeap常見的操作

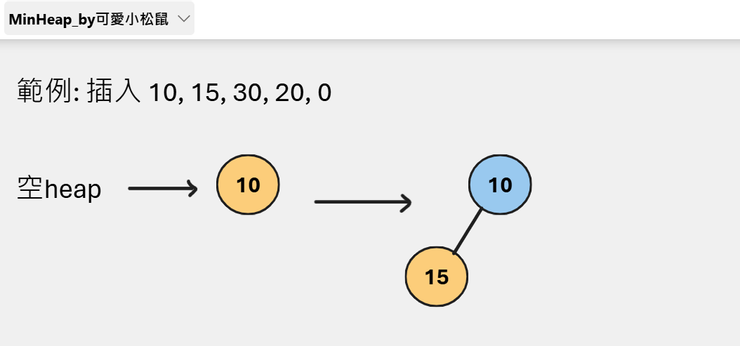
1.插入節點 insert(data)

將新元素插入到堆的最後一個位置。

比較此元素和父節點的值，如果新元素比父節點還小則需要交換位置，
直到不能再向上移動為止。

時間複雜度: O( log n )

  def insert(self, data):
  
    self.heap.append(data)
    self._heapify_up(len(self.heap) - 1)

2.向上調整 _heapify_up(index)

檢查heap[index]指定的元素，如果比父節點還小，就向上調整到正確的位置。

來滿足Min Heap每個節點的值都小於或等於其子節點的值的規定。

時間複雜度: O( log n )

  def insert(self, data):
    self.heap.append(data)
    self._heapify_up(len(self.heap) - 1)

  def _heapify_up(self, index):
    parent_index = (index - 1) // 2

    if index > 0 and self.heap[index] < self.heap[parent_index]:
      self.heap[index], self.heap[parent_index] = self.heap[parent_index], self.heap[index]
      self._heapify_up(parent_index)
    return

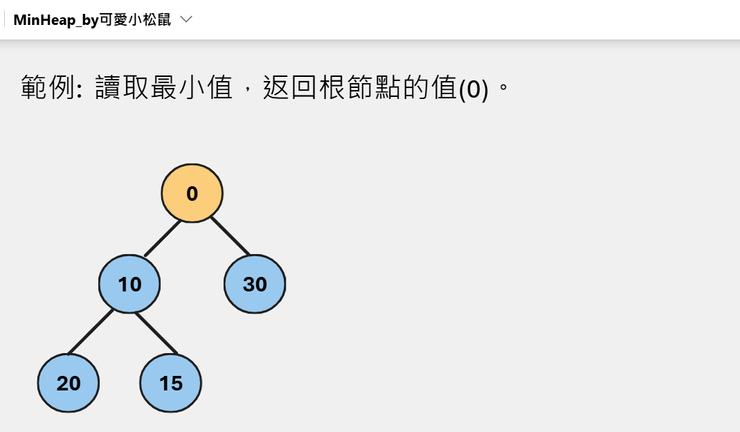
3.讀取最小值 get_min()

讀取整個堆積heap的最小值，也就是讀取根節點的值。

時間複雜度: O( 1 )

  def get_min(self):
    if len(self.heap) == 0:
        return None
    return self.heap[0]

4.取出最小值 extract_min()

取出根節點（最小值），並將最後一個元素移到頂端，填補空缺，當作新的根節點。

比較新的根節點和其子節點的值，若有需要則交換位置，直到不能再向下移動為止。

時間複雜度: O( log n )

5.向下調整 _heapify_down(index)

檢查heap[index]指定的元素，如果比子節點還大，就向下調整到正確的位置。

來滿足Min Heap每個節點的值都小於或等於其子節點的值的規定。

時間複雜度: O( log n )

  def extract_min(self):
    if len(self.heap) == 0:
      return None
    if len(self.heap) == 1:
      return self.heap.pop()

    root = self.heap[0]
    self.heap[0] = self.heap.pop()
    self._heapify_down(0)
    return root


  def _heapify_down(self, index):
    smallest = index
    left_child_index = 2 * index + 1
    right_child_index = 2 * index + 2

    if left_child_index < len(self.heap) and self.heap[left_child_index] < self.heap[smallest]:
      smallest = left_child_index
    if right_child_index < len(self.heap) and self.heap[right_child_index] < self.heap[smallest]:
      smallest = right_child_index

    if smallest != index:
      self.heap[index], self.heap[smallest] = self.heap[smallest], self.heap[index]
      self._heapify_down(smallest)

    return

6.取得堆積heap的大小 size()

取得堆積的大小 = 堆積內的資料總數量。

時間複雜度: O( 1 )

  def size(self):
    return len(self.heap)

測試範例

完整的Min Heap實作和程式碼

class MinHeap:
  def __init__(self):
    # 初始化時，是一個空的堆積empty heap
    self.heap = []

  def insert(self, data):
    self.heap.append(data)
    self._heapify_up(len(self.heap) - 1)

  def extract_min(self):
    if len(self.heap) == 0:
      return None
    if len(self.heap) == 1:
      return self.heap.pop()

    root = self.heap[0]
    self.heap[0] = self.heap.pop()
    self._heapify_down(0)
    return root

  def _heapify_up(self, index):
    parent_index = (index - 1) // 2

    if index > 0 and self.heap[index] < self.heap[parent_index]:
      self.heap[index], self.heap[parent_index] = self.heap[parent_index], self.heap[index]
      self._heapify_up(parent_index)
    return

  def _heapify_down(self, index):
    smallest = index
    left_child_index = 2 * index + 1
    right_child_index = 2 * index + 2

    if left_child_index < len(self.heap) and self.heap[left_child_index] < self.heap[smallest]:
      smallest = left_child_index
    if right_child_index < len(self.heap) and self.heap[right_child_index] < self.heap[smallest]:
      smallest = right_child_index

    if smallest != index:
      self.heap[index], self.heap[smallest] = self.heap[smallest], self.heap[index]
      self._heapify_down(smallest)

    return

  def get_min(self):
    if len(self.heap) == 0:
        return None
    return self.heap[0]

  def size(self):
    return len(self.heap)

def test():
  # Demo code
  min_heap = MinHeap()
  min_heap.insert(10)
  min_heap.insert(15)
  min_heap.insert(30)
  min_heap.insert(20)
  min_heap.insert(0)

  print("Min element:", min_heap.get_min())  # Output: 0
  print("Extracted min element:", min_heap.extract_min())  # Output: 0
  print("Min element after extraction:", min_heap.get_min())  # Output: 10
  print("Heap size:", min_heap.size())  # Output: 4

if __name__ == '__main__':

  test()

測試輸出

Min element: 0
Extracted min element: 0
Min element after extraction: 10
Heap size: 4

結語

其實Tree就是Node的組合與推廣，每個節點最多可以有兩個子節點的樹狀資料結構。

而Min Heap就是Binary Tree額外限制上層節點值 永遠小於 下層節點值的規則。

讀者可以透過紙筆追蹤演算法和程式執行邏輯，測試幾個簡單的小範例，

會有更深刻的了解和體會！

Heap相關的演算法練習題與詳解

六六大順 能不能製造出順子? Hand of Straights 堆積/排序應用_Leetcode #846

實作餐廳訂位報號系統 Seat Reservation Manager Leetcode #1845

模擬: 最遠可以抵達的大樓 Furthest Building You Can Reach_Leetcode #142

滄海一粟 第k小的分數(最小堆+生成應用) Leetcode #786

最小堆應用: 雇用k名員工的最小成本 Total Cost to Hire K Workers #2462 精選75題

系統設計: 動態取出數據流的最小值 Leetcode #2336_Leetcode 精選75題解析