舊業重溫13--有特別內角的三角形求面積

[陳傳義]拍攝

本篇求解的題目也是在YT找到的,算是上一篇《舊業重溫12--有內角平分線的直角三角形求面積》的續篇,同樣分別提供國中的古典幾何和高中的三角函數解法。
本題跟上一篇都是求三角形面積,所不同者,本題並非直角三角形,但有一個值得注意的角度, 45°,這是國中、高中數學都重視的特殊角度。

題目:

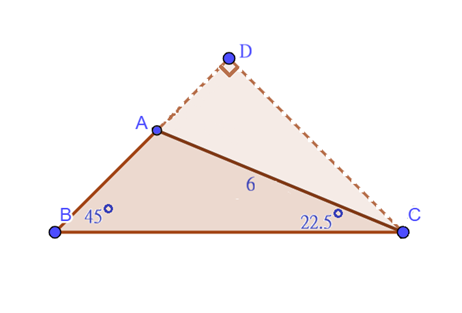
圖一

∠B=45°,∠C=22.5°, AC邊長6,

求△ABC面積。

解法一:

見到求三角形面積,該當想到底×高÷2。但本題沒有直角,不像前一題那般自然地暗示底和高。但上一篇提到,古典幾何解題常須作輔助線,我們可以作出某一邊的高試試。

圖二

注意已知條件裡,∠B=45°是特別角。如果過C向BA邊作高(垂直線),垂足D落在BA的延長線上。

( 參考圖二,讀友們看出甚麼好事發生了嗎? ... )

∠DCB=180° - 45° - 90° = 45° =∠B,
∴△DBC是等腰直角三角形, 於是
BD長：DC長：BC長=1：1：√2,
另外,
∠DCA=∠DCB -∠ACB=45° - 22.5° = 22.5° =∠ACB, 亦即AC是∠DCB的分角線,
引用上一篇末尾證明的「內分比定理」,得到
DA長：AB長 = DC長：BC長 = 1：√2,
假設AD長 = s, 則BA長 =√2 s, 則
DC長=BD長=BA長 + AD長 = √2 s + s =(√2 + 1)s

∵△ADC是直角三角形,根據畢氏定理, s² + (√2 + 1)²s² = 6²
∴ ( 1 + 2 + 2√2 + 1)s² = 36, 合併得 (4 + 2√2)s² = 36, 等式兩邊同除以2, 得到
   (2 +√2)s² = 18 …… (ㄅ)

∴△ABC面積 = AB長 × CD長 ÷ 2
             =√2 s × (√2 + 1)s ÷ 2 = ((√2)² + √2)s²
             =(2 +√2)s² ÷ 2   (引用(ㄅ)的結果)
             = 18÷2 = 9

解法二:

圖三

如果過A向BC邊作高AD(參考圖三),也可行。以下借助高中三角函數的一些知識。

設θ=22.5°, 則2θ= 45°,
在直角△ADC中,
由正、餘弦函數定義,推得
AD長= 6sinθ, CD長= 6cosθ,
而△ABD是等腰直角三角形,
所以BD長 = AD長 = 6sinθ,
∴ BC長 = BD長 + CD長 = 6sinθ+ 6cosθ = 6(sinθ+ cosθ)

∴ △ABC面積 = BC長 × AD長 ÷ 2
= 6(sinθ+cosθ) × 6sinθ÷ 2

= 9×1 = 9

解法三:

如果利用深入一些的三角函數性質,也可以不必作輔助線。(請參考圖一)

依據正弦定理--三角形各內角的正弦值與其對邊長比例相等,

又∠A=180° - 45° - 22.5° = 112.5°,

套用高中學過的「兩邊長及其夾角求三角形面積公式」,
△ABC面積 =AB長 × AC長 × sinA ÷ 2

註1: 餘弦函數二倍角公式 cos2θ= 1-2sin²θ= 2cos²θ-1
     正弦函數二倍角公式 sin2θ= 2sinθcosθ

註2: 廣義角大角化成小角的規則 sin(90°+θ)=cosθ,  cos(90°+θ)= -sinθ