使用Excel計算數值分散趨勢

假設您目前即將接任教務主任一職，您想要知道甲班與乙班的學生在整個學期中的學習成果，是甲班較出色，還是乙班的同學較認真？此時，身為教務主任的您，在收集了學生的學期成績後，要如何進行比較，才能公平的判斷出兩班同學的程度差異及同一班的學生，普遍程度都落在哪個成績水準上？

要得到這個問題的答案，最好的方法，就是先個別觀察各班同學的平均成績水準，接著，再依此成績進行班級間的比較，將會精準的比較出兩班同學的學習成果差異。

也就是說，當我們搜集了一串統計資料後，利用整理的方法，有時並無法精準的找到我們想要的答案，此時，您就必須利用計算的方式，求得您所要的答案。

3-1 未分組資料中央集中趨勢的衡量

當我們想要知道台灣與新加坡的國民的消費能力，孰高孰低時，通常，我們會使用國民平均所得，做為比較的基準。所得愈高的國家，表示國民的消費能力愈高，愈低，則可能意謂著這個國家，國民生活水準普遍低落。而「國民平均所得」，則意謂著這個國家所有國民所得的平均數值，當個人的所得較國民平均所得高時，則表示個人收入高於平均水準，屬於高收入的族群之一，反之，則可能列為低收入族群當中。當然，若我們只想要知道台灣地區人民的貧富差距情形，藉由觀察資料的分佈情況及集中趨勢，則有助於我們對於整體情況的了解。

一般用來測量中央趨勢(即數列的中心點)的指標有三種，即平均數、中位數及眾數。它們可用來代表資料的分佈情形及分配方法。

平均數

平均數是用來衡量資料的中央集中趨勢最重要的指標。它除了可以用來表示一組資料的平均水準之外，亦可做為比較兩組或兩組以上資料的平均水準。

當我們要計算出某一數列的算數平均數時，只要把每個值進行加總，再除以個數即可。您可以參考下列的公式。

X=(X₁+X₂+……+X_N)/N

就如在上述的例子當中，若新任的教務主任想要知道一年甲班及一年乙班在電腦學科上哪一班的程度較佳時，則可分別計算出兩班的平均分數，再進行比較即可。

應用範例：計算數列的平均數

在此範例中，我們將分別計算出一年甲班及乙班的學期成績平均數，以便做出比較。

1. 開啟一空白活頁簿，並分別輸入兩班同學的成績。使用滑鼠選取我們要放置甲班平均成績的儲存格「H5」。選取「公式Formula、statistic 」。
2. 在清單中，選取「AVERAGE」算數平均數函數，並按下「確定」鍵。在「Number」欄中輸入甲班全部同學的成績儲存格範圍「C3:C62」後，按下「確定」，您即會在H5儲存格欄位中看到甲班同學的平均成績。

重複上述的步驟，在「I5」儲存格中插入AVERAGE函數，即可計算出乙班同學的成績為66.3。

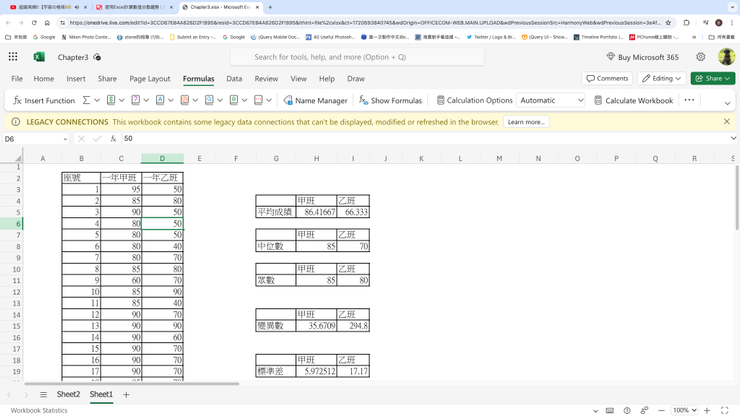
而在此例中，我們可以看到甲班的平均成績為「86」分，乙班的成績為「66」分，因此可以判定甲班的學習成果較乙班為｢佳｣。

中位數

利用平均數來求得整體的平均水準，雖然不失為一個比較整體水準的好方法，但倘若在數列當中，存在著太多極端值時，則整體水準可能因此而被拉低。此時，您可以選擇使用中位數來做為中央趨勢的指標。

所謂中位數(m_e)，指的就是所得來的資料，經由小排到大的順序排列，居於數列最中央的那個數值，則為中位數。當我們要求得一數列的中位數時，首先要注意的是您的數列數值個數若為單數時，中位數為依序排列的數列中第(N+1)/2的那個數值；若您的數列數值個數為偶數時，則取(N+1)/2前後兩個數為中位數。

在數列數值不多時，我們可以很快的就計算出中位數的內容，但假設我們有一千筆資料時，計算上，就會耗費很大的功夫。此時，您可以利用MEDIAN()函數，快速的為我們求出數列的中位數。

範例實做：求取中位數

為了更暸解甲、乙兩班的程度，教務主任決定算出甲、乙兩班同學的中位數各為何？

使用滑鼠選取我們要放置甲班中位數資料的儲存格「H8」，輸入「MEDIAN＝C3:C62」後，按下「確定」，您即會在H8儲存格欄位中看到所求得的甲班同學成績的中位數為85。

最後，我們可以重複上述的步驟，在「I8」儲存格中插入MEDIA函數，並指定儲存格範圍為「D3:D62」即可計算出乙班同學的成績中位數為70。

在分別算出了甲、乙班同學成績的中位數後，我們可以看到甲班的中位數及平均數相當的相近；而乙班同學的平均成績及中位數相差了約4分，表示在乙班同學的成績中包含有極值，拉低了平均數。

眾數

眾數，指的是觀察值中出現次數最多的那一個數值，或者是那一個類別，也可以是用來衡量集中趨勢的一個指標。

一般而言，由於眾數指的是所有觀察值中出現次數最多的那一個數值，所以，它不會像平均數一樣受到極端值的影響，對觀察值的數值變化的感應程度，也相當的不靈敏。而在求取眾數的過程中，您可能會發現，眾數可能會出現多個眾數或者是沒有眾數的情況，因此，在用來求取數值的集中趨勢時，眾數較中位數或者是平均數來的少用。

而在下面的圖中，您可以看到在一串數列當中，40及50所出現的次數各為三次，所以此一數列的眾數為40及50。

要求出一數列的眾數值，其實不難，而在Excel工作表中，若我們想要求出一數列中的眾值時，我們則可以使用MODE函數，來求得眾數值的內容。

範例實做：求取眾數值

若教務主任決定利用眾數，來觀察甲、乙兩班同學的成績分佈中央趨勢時，他應該如何著手？

1. 使用滑鼠選取我們要放置甲班中位數資料的儲存格「H11」，並輸入「MODE＝C3:C62」後，按下「確定」。

您即會在H11儲存格欄位中看到所求得的甲班同學成績的眾數值為85。

 最後，我們可以重複上述的步驟，在「I11」儲存格中插入MODE函數，並指定儲存格範圍為「D3:D62」即可計算出乙班同學的成績中位數為80。

 偏態觀察

在得出觀察值的中心點，我們可以分別的計算出平均數、中位數及眾數等數值，但倘若我們想要對此數列做通盤的暸解時，則可以繪製圖表，觀察這些觀察值的集中趨勢及分佈情況。

在Excel中，若我們想要進一步的將數列中的每個觀察值整理為一個數值分佈圖表時，我們可以利用樞紐分析表工具先計算出數值分佈的次數，接著再透過樞紐分析圖表精靈，繪製出分佈圖。承接上面的例子，在下面的操作實例中，我們將為甲班及乙班同學的成績，分別製作出數值分佈圖表，提供觀察者做為進一步的參考。

實做範例：使用樞紐分析工具製作分佈圖

在本範例中，我們將使用樞紐分析工具製作出甲班同學成績的分佈圖。

1. 開啟包含有甲班同學成績資料的活頁簿，並選取「Insert 插入、Pivot Table樞紐分析表及圖報表」，開啟「建立樞鈕分析表」對話窗。

 2.在「樞紐分析表精靈」的步驟3之2中，選取所要建立的樞鈕分析表的數值資料範圍。

 3..在新增的空白樞紐分析表中，以拖曳的方式將「一年甲班」拖曳到「列」欄位及「資料欄位」等位置。

 4.選取合計欄位，選取｢COUNT｣，讓數值成為計次。

1. 由於我們希望以圖表的方式呈現數值，因此，請選取圖表範圍。選取｢Insert 插入、圖表｣，選取我們要的圖形｢直條圖｣，即可完成分佈圖之製作工作。

最後，您可以看到在所產生的次數分佈圖中，甲班同學的成績分佈相當的平均，分數分佈集中在60-95分之間。全班平均素質算是相當的集中。

數值選擇

不論是平均數、中位數或者是眾數，三者都可以用來表現中央集中趨勢的指標。使用者可以依照自己的用途，決定要使用哪種計算方式。

一般而言，在觀察值中無極端值資料或偏態時，您可以採用平均數做為指標；而在觀察值中，若存在著極端值或具偏態的狀況時，您則可以考慮採用中位數，做為中央集中趨勢的指標。

3-2 數值的離散程度計算 

當我們想要比較二個數列之間的差異程度時，我們會透過以大濟小、削高就低的方式，計算出一個數值，來代表此一數列，以便與同類事物的其他數列的平均水準進行比較，而此數值即為我們所謂的平均數。

平均數雖然是數列中的每個變數所計算出來的，但每個變數並不等於平均數，它們與平均數之間都存在者一個距離，有的大些、有的小些，此時，若我們想要知道這些數值的平均離散程度，就會再求出一個平均離差來代表這個數例的變動性大小。此時，我們就可以採用變異收及標準差，來說明數列的離散程度。

變異數

所有觀察值減去平均數的平方和，再除以觀察值的變數個數所得出的數值，即為變異數。當我們所計算出來的變異數值愈大時，表示變異程度愈大，反之則愈小，但倘若所計算出來的變異數值等於零時，則表示所有的觀察值均相同，並沒有分散。

若是我們要求出樣本的變異數時，則必須把所有觀察值與樣本平均數離差的平方和除以觀察值的個數減一。

接著，讓我們延續上面的成績範例，來看看甲班與乙班每位同學成績的離散程度。

範例實做：計算甲班及乙班成績之變異數

在本範例中，我們將利用VAR函數，分別求出甲班及乙班同學成績的變異數。

1. 使用滑鼠選取我們要放置甲班變異數資料的儲存格「H15」，輸入公式，並指定範圍是甲班全部同學的成績儲存格範圍「C3:C62」後，按下「確定」，您即會在H15儲存格欄位中看到甲班的成績變異數為「35.6709」。

在這裡，若我們想要快速的求得乙班同學的變異數，我們可以使用複制的方法，直接將滑鼠游標停放在H15儲存格上，並使用滑鼠選取功能表中的「編輯、複製」選項，表示複製H15中的公式。最後，再將滑鼠游標停放在I15儲存格當中，並選取「編輯、貼上」，即可求得乙班的變異數內容「294.8」。

由此可知，乙班同學的變異程度較大，素質較不一。

標準差

由於變異數涉及平方和，故其單位應為測量單位的平方。舉個例子來說，若觀察值的單位為公斤時，則求得的變異數單位即為(公斤)²，所以，欲求得與計量資料相同單位的離差，就必須把變異數值開根號，而所得的數值即為標準差。

而所求出的標準差愈大，則表示觀察值的變動性愈大，平均數代表性小；反之，所求出的觀察值愈小，則表示變動性愈小，平均數的代表性大。

就如在投資證券市場時，我們則可以利用標準差，做為估量風險大小的尺度。例如，我們想要評估甲、乙兩家公司的股票投資風險時，我們利用甲公司股票年收益率的10年資料，求得平均收益率為7％，並計算出其標準差為5.3％，即表示甲公司股票的收益率為7％±5.3％，其變動範圍在12.3～1.7％之間。

同樣的，我們再收集乙公司10年的收益率資料，計算出其10年的平均收益率同樣的也是7％，但標準差卻為是6.4％，則乙公司的年收益率為7％±6.4％。在比較投資這兩家公司的風險時，顯示投資乙公司股票的風險要比甲公司為高。

而在Excel中，若我們想要求得數列的標準差時，我們可以採用STDEV函數，來求得標準差的值。

範例實做：計算甲班及乙班成績之標準差

在本範例中，我們將利用STDEV函數，分別求出甲班及乙班同學成績的標準差。

1.使用滑鼠選取我們要放置甲班變異數資料的儲存格「H18」，並輸入公式「STDEV(C3:C62)」，您即會在H15儲存格欄位中看到甲班的成績的標準差為「5.972512」。最後，我們再用複製的方法，直接將H18的公式複制到儲存格I18中，即可求得乙班的變異數內容「17.17」。

說明：除了利用函數來求得這些數值外，我們還可以使用Excel中的「增益集」，快速的求得以上的各種數值。