
大家應該都實際練習過機器學習的四大技術了,包含迴歸分析、分類分析、分群分析以及時間序列分析。 在機器學習模型的開發過程中,我們常將焦點放在演算法的選擇與模型的訓練上,但實際上,一個高效且穩健的模型,往往取決於資料的前處理與特徵的設計。隨著模型複雜度提升,過擬合、特徵尺度不一致以及高維資料噪聲等問題會逐漸顯現。若未妥善處理,模型再強大也可能表現不佳。
📝 為什麼要使用正則化/歸一化技巧?
在機器學習模型訓練中,我們經常面臨幾個核心挑戰,這些挑戰可能嚴重影響模型的性能和泛化能力:
問題一:過擬合(Overfitting)
模型在訓練數據上表現優異,但在測試數據上表現不佳。這是因為模型過度記憶了訓練數據中的細節和噪音,失去了將學習內容應用到新數據的能力。當模型變得過於複雜,有太多參數可以調整時,容易發生這種情況。問題 2:不同特徵的重要性受到數值範圍影響
當數據包含不同尺度的特徵時(例如一個特徵範圍是 [0, 1],另一個是 [0, 10000]),大範圍特徵可能會主導模型學習過程,使得小範圍特徵的重要信息被忽略,即使它們在實際應用中可能更加關鍵。這種不平衡會導致梯度下降等優化算法難以找到最佳解。
問題 3:訓練過程過慢或不穩定
深度學習模型通常需要大量時間才能收斂,並且可能因為初始權重設置不當而表現不穩定,甚至出現梯度消失或梯度爆炸等數值問題。這些問題會嚴重影響訓練效率,甚至導致訓練失敗。
問題 4:高維數據導致模型挑戰
隨著特徵數量增加,模型參數也隨之增加,造成”維度災難”問題。這會導致模型過於複雜,容易受噪聲影響,且難以高效識別重要特徵。在高維空間中,數據變得稀疏,使得模型更難以捕捉真實的數據分布。
如何解決?
正則化 (Regularization)
正則化的核心目的是解決過擬合問題,它通過對模型複雜度施加限制,確保模型不僅能記住訓練數據,還能學習數據的真實模式。正則化還可以:
- 自動進行特徵選擇,抑制不重要特徵的權重,讓模型更加專注於重要特徵
- 提高模型穩定性和泛化能力,使其在新數據上表現更佳
- 簡化模型結構,增強可解釋性,避免”黑盒子”效應
- 在多個解同樣適合訓練數據的情況下,選擇最簡單的解
歸一化 (Normalization)
歸一化的核心目的是解決特徵尺度差異問題,它通過重新縮放數據,使所有特徵處於相似的數值範圍。歸一化能夠:
- 確保模型公平地評估每個特徵的重要性,不受原始數值大小影響
- 加速模型訓練過程並提高收斂穩定性,特別是使用梯度下降的算法
- 減少初始化敏感性,使訓練結果更一致,提高實驗的可重複性
- 在深度學習中,批次歸一化還能穩定各層的激活分布,防止內部協變量偏移問題
📚 正則化 (Regularization)
正則化是一種控制模型複雜度的數學方法,旨在防止模型過度擬合訓練數據。當模型過於複雜時,它可能會學習到訓練數據中的雜訊而非真實模式,導致泛化能力下降。正則化通過在損失函數中加入懲罰項,限制模型參數的大小或數量,從而鼓勵模型保持簡單。
從貝葉斯統計學角度來看,正則化可以被視為對模型參數的先驗概率分布的假設。L1正則化相當於假設參數服從拉普拉斯分布(偏好稀疏),而L2正則化則相當於假設參數服從高斯分布(偏好小值)。
💡實作方法可以參考sklearn.linear_model中的Lasso、Ridge和ElasticNet
L1 正則化 (Lasso Regression)
L1正則化通過在損失函數中加入參數絕對值之和的懲罰項,鼓勵模型產生稀疏解。

核心特點:
- 能夠將不重要特徵的權重壓縮為零,自動進行特徵選擇
適用場景:
- 需要自動選擇重要特徵的高維數據集
- 懷疑數據中存在許多無關特徵時
- 追求模型簡單性和可解釋性時
- 面對高度稀疏的問題(如文本分析)
優缺點:
- ✅ 可實現特徵自動選擇,產生稀疏解
- ✅ 減少過擬合,提高模型解釋性
- ✅ 內建特徵選擇功能,簡化後續分析
- ❌ 在特徵高度相關時,可能隨機選擇其中一個
- ❌ 優化過程可能不如L2穩定,因為L1導數不連續
L2 正則化 (Ridge Regression)
L2正則化通過在損失函數中加入參數平方和的懲罰項,鼓勵所有權重保持較小的數值。

核心特點:
- 促使所有參數均勻縮小,但通常不會為零
適用場景:
- 處理多重共線性問題(特徵間高度相關)
- 希望所有特徵都保留在模型中
- 需要穩定模型解的場景
- 數據中存在高度噪聲但大部分特徵都有一定預測價值
優缺點:
- ✅ 數學性質良好,優化過程穩定(凸優化問題)
- ✅ 有效處理特徵間高度相關的問題
- ✅ 對所有特徵提供平滑的懲罰,不會完全消除任何特徵
- ❌ 不會產生稀疏解,難以自動選擇特徵
- ❌ 當只有少數特徵重要時,可能表現不如L1
Elastic Net
Elastic Net結合了L1和L2正則化的優點,通過同時使用兩種懲罰項,平衡穩定性和稀疏性。

核心特點:
- 同時具備特徵選擇能力和穩定性
適用場景:
- 特徵數量大於樣本數的情況(p > n問題)
- 特徵間存在高度相關性的群組
- 需要兼顧特徵選擇和穩定性時
- 不確定L1還是L2更適合問題時
優缺點:
- ✅ 結合L1和L2的優點,提供更靈活的正則化框架
- ✅ 在特徵相關性高時表現優於單純的L1
- ✅ 當特徵數遠大於樣本數時尤其有效
- ❌ 需要調整兩個超參數,增加調參難度
- ❌ 計算成本略高於單一正則化方法
為什麼L1可以用於特徵篩選而L2不能?
L1和L2正則化對模型權重的影響機制完全不同,這導致了它們在特徵選擇能力上的差異:
L1正則化的幾何解釋

- 懲罰形式:構成了參數空間中的菱形約束區域
- 稀疏性機制:當損失函數的等高線與L1約束的菱形相交時,交點通常落在坐標軸上,意味著部分權重精確地等於零
- 視覺化:在二維空間中,L1約束區域是一個菱形,其頂點位於坐標軸上
L2正則化的幾何解釋
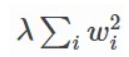
- 懲罰形式:構成了參數空間中的圓形(或超球面)約束區域
- 收縮機制:當損失函數的等高線與L2約束的圓形相交時,交點很少會落在坐標軸上,導致權重接近零但不等於零
- 視覺化:在二維空間中,L2約束區域是一個圓形,沒有明顯的角點
數學視角的解釋
L1正則化對於小權重的梯度恆定(常數),而L2正則化對於小權重的梯度變小。這意味著:
- 使用L1時,即使權重很小,也會持續受到恆定的壓力向零收縮,直至變為精確的零
- 使用L2時,權重越小,收縮壓力越小,導致權重接近零但很難達到精確的零
此外,從優化角度看,L1項在零點處不可微分,這一特性使得優化過程更容易將不重要的參數推至恰好為零,而不是接近零的小值。
🌈 歸一化(Normalization)
歸一化是調整特徵數值尺度的過程,將不同範圍的數據轉換到統一的標準範圍內。適當的歸一化可以加速訓練過程、提高收斂穩定性,並確保所有特徵能被模型公平對待。
Min-Max 歸一化
Min-Max歸一化將數據線性變換到一個固定範圍內,最常用的是[0,1]區間。

核心特點:
- 保留原始數據分佈形狀,只改變尺度
適用場景:
- 特徵邊界明確的情況
- 需要保留零值的場景
- 神經網絡中使用sigmoid激活函數時
- 視覺化和直觀比較不同尺度的特徵
優缺點:
- ✅ 直觀易懂,結果具有明確界限
- ✅ 保留原始數據分佈特性和相對關係
- ✅ 處理後的數據界限明確,便於後續處理
- ❌ 對異常值極其敏感,少量極端值可能壓縮大部分數據
- ❌ 在數據持續更新的場景中,可能需要重新計算最大最小值
標準化(Standardization)
標準化將數據轉換為均值為0,標準差為1的分佈,也稱為Z-score歸一化。

核心特點:
- 轉換後的數據呈標準正態分佈(如果原數據為正態分佈)
適用場景:
- 原始數據分佈近似正態分佈
- 對異常值敏感的算法(如SVM、KNN)
- 使用L1/L2正則化的模型
- PCA等依賴特徵方差的技術
優缺點:
- ✅ 對異常值不敏感,提高模型穩定性
- ✅ 適用於大多數機器學習算法,特別是基於距離或梯度的方法
- ✅ 便於不同特徵間的比較和解釋
- ❌ 不保證數據落在特定範圍內,可能產生極端值
- ❌ 如果原始數據不是正態分佈,轉換後也不會是標準正態分佈
批次歸一化(Batch Normalization)
批次歸一化是為深度神經網絡設計的歸一化技術,它在每個小批次(mini-batch)中對網絡層的輸入進行標準化處理。
核心特點:
- 在網絡訓練過程中動態調整每層的輸入分佈
工作原理:
- 減少內部協變量偏移(Internal Covariate Shift),使每層的輸入分佈更穩定
- 添加可學習的縮放和偏移參數,保持網絡的表達能力
- 在推理階段使用整個訓練集的統計信息
適用場景:
- 深度神經網絡訓練
- 希望減少訓練時間
- 需要使用較大學習率的場景
- 減輕對初始化方法的依賴
優缺點:
- ✅ 加速網絡收斂,允許使用更高學習率
- ✅ 減輕梯度消失/爆炸問題
- ✅ 降低初始化敏感性
- ✅ 具有輕微正則化效果
- ❌ 增加計算複雜度和內存消耗
- ❌ 在小批量情況下可能表現不穩定
- ❌ 在循環神經網絡等時序模型中效果可能不佳
數學流程:
- 計算批次均值

- 計算批次方差

- 標準化

- 縮放和平移

技術比較

正則化vs歸一化:核心區別

正則化和歸一化的協同作用
正則化和歸一化並非互斥技術,而是互補的優化策略。在實際應用中,它們通常一起使用以獲得最佳結果:
- 歸一化後正則化更有效:當特徵尺度一致時,正則化懲罰項能更公平地評估和控制所有特徵權重
- 聯合使用效果最佳:實驗表明,同時使用歸一化和適當的正則化通常會得到泛化能力最強的模型
- 不同階段的優化:歸一化主要作為數據預處理步驟,而正則化則作為模型訓練過程的一部分
- 解決不同層面的問題:歸一化解決數據層面的尺度不一致問題,正則化解決模型層面的過度複雜問題
實際應用建議
- 從基礎開始:對任何機器學習項目,首先應用適當的歸一化方法處理數據
- 逐步添加正則化:然後嘗試不同強度的正則化,通過交叉驗證找到最佳參數
- 監控驗證性能:觀察訓練和驗證性能間的差距,判斷模型是否過擬合或欠擬合
- 針對問題選擇技術:高維稀疏數據可能更適合L1正則化,而特徵間高度相關的數據可能更適合L2正則化
通過合理結合這兩種技術,可以顯著提高機器學習模型的性能、穩定性和泛化能力。






















