統計檢定方法運用.5
閱讀時間約 1 分鐘
Durbin-Watson test，對模組的殘差項進行相關聯性檢定，常應用於迴歸分析以及需要限制殘差項要為獨立常態分配。不過我在應用上更關心價格資料是否有聚集在均線附近，若有則可以判定盤整盤，反之則有趨勢發生，相關統計檢定計算步驟詳列如下
- 以均線為例，首先計算出各筆價格與均線之間的殘差，並帶入檢定統計量，請參考下圖一
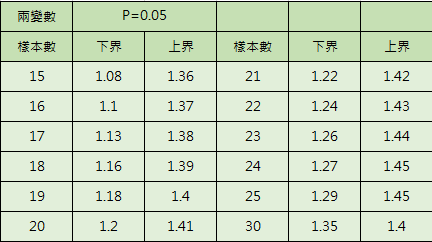
- 統計檢定量介於0~4之間，正相關、負相關檢定與對應的上界、下界，分別有六種關係，
正相關時候
如果d <= 下界 ，誤差項自我相關為正
如果d >= 上界 ，不拒絕，無自我相關
如果下界 < d < 上界 ，則檢定結果無法確認
負相關時候
如果(4 - d) <= 下界 ，誤差項自我相關為負
如果(4 - d) >= 上界，不拒絕，無自我相關
如果下界 < (4 - d) < 上界 ，則檢定結果無法確認
如果d <= 下界 ，誤差項自我相關為正
如果d >= 上界 ，不拒絕，無自我相關
如果下界 < d < 上界 ，則檢定結果無法確認
負相關時候
如果(4 - d) <= 下界 ，誤差項自我相關為負
如果(4 - d) >= 上界，不拒絕，無自我相關
如果下界 < (4 - d) < 上界 ，則檢定結果無法確認
3. 上界、下界請參考查表值，以下僅列舉一個變數、樣本數介於15~30之間、顯著水準為0.05的部分查表內容
為什麼會看到廣告
21會員
112內容數
留言0
查看全部
你可能也想看
Google News 追蹤
1.資金水位測試：資金比重是不是太高？有沒有做風險控管？
2.持股強弱測試：個股是回檔還是回跌？跌的有沒有比指數重？
3.心理素質測試：情緒有沒有失控？停損底線是甚麼？
4.交易週期測試：真的長線投資者嗎？長線投資策略有沒有瑕疵？如果指數再跌更重，因應策略是甚麼？
本研究使用了盤中逐筆成交資料（Tick-by-tick Data）來進行股票價格的預測，並討論了馬可夫鏈模型和擴散核模型在這方面的應用。研究結果表明，大多數股票的未來三秒價格可以在少於22個狀態中找到，顯示了交易價格的低不確定性。此外，研究還發現波動性更大和價格更高的股票更難以準確預測。
緩解與未緩解是訂單流的核心概念，簡單來說就是透過識別未緩解區域，了解主力和大量訂單的入場位置。
什麼是緩解與未緩解？
未緩解指的是在一段時間中市場效率低下，買單和賣單的無法相互匹配成交時，會在市場形成一個價位的空洞，就會將其稱之為未緩解。
如上圖所繪，中間K線未與上下K線所重疊，其中K線空洞的
前面說明了所謂「假設檢定」的邏輯，也就是推論統計的基礎。但前面都還只是概念的階段，目前沒有真正進行任何的操作──還沒有提到推論統計的技術。
這篇其實有點像是一個過渡，是將前面的概念銜接到下一篇t分數之間的過程，也可以說是稍微解釋一下t檢定怎麼發展出來的。
接續上一篇，繼續來講如何從常態分布的機率進行假設檢定，進而推論母體的平均數吧！
這篇會提到否證的邏輯、魔法數字0.5以及統計檢定到底是什麼這三個主題。
當開啟試算表（EXCEL等）的累加（SUM）及離散度，標準差（STDEV）的運算功能後，逐一統計的累進報票式選票統計表就可以退休了，而且全國一萬七千多所的數據不待一所所列出，就可以用較小選區（例如嘉義市198所，宜蘭縣431所等）的統計過程證明統計結果都是正確的，尤其是將計算式列出（隱藏前面的
在上一篇文章解釋了常態分布怎麼幫助我們計算事件發生的機率，而更之前也看過了抽樣分布是如何形成常態分布的過程，現在就要利用這兩件事情來慢慢帶出什麼是統計學中的「假設檢定」了。
1.資金水位測試：資金比重是不是太高？有沒有做風險控管？
2.持股強弱測試：個股是回檔還是回跌？跌的有沒有比指數重？
3.心理素質測試：情緒有沒有失控？停損底線是甚麼？
4.交易週期測試：真的長線投資者嗎？長線投資策略有沒有瑕疵？如果指數再跌更重，因應策略是甚麼？
本研究使用了盤中逐筆成交資料（Tick-by-tick Data）來進行股票價格的預測，並討論了馬可夫鏈模型和擴散核模型在這方面的應用。研究結果表明，大多數股票的未來三秒價格可以在少於22個狀態中找到，顯示了交易價格的低不確定性。此外，研究還發現波動性更大和價格更高的股票更難以準確預測。
緩解與未緩解是訂單流的核心概念，簡單來說就是透過識別未緩解區域，了解主力和大量訂單的入場位置。
什麼是緩解與未緩解？
未緩解指的是在一段時間中市場效率低下，買單和賣單的無法相互匹配成交時，會在市場形成一個價位的空洞，就會將其稱之為未緩解。
如上圖所繪，中間K線未與上下K線所重疊，其中K線空洞的
前面說明了所謂「假設檢定」的邏輯，也就是推論統計的基礎。但前面都還只是概念的階段，目前沒有真正進行任何的操作──還沒有提到推論統計的技術。
這篇其實有點像是一個過渡，是將前面的概念銜接到下一篇t分數之間的過程，也可以說是稍微解釋一下t檢定怎麼發展出來的。
接續上一篇，繼續來講如何從常態分布的機率進行假設檢定，進而推論母體的平均數吧！
這篇會提到否證的邏輯、魔法數字0.5以及統計檢定到底是什麼這三個主題。
當開啟試算表（EXCEL等）的累加（SUM）及離散度，標準差（STDEV）的運算功能後，逐一統計的累進報票式選票統計表就可以退休了，而且全國一萬七千多所的數據不待一所所列出，就可以用較小選區（例如嘉義市198所，宜蘭縣431所等）的統計過程證明統計結果都是正確的，尤其是將計算式列出（隱藏前面的
在上一篇文章解釋了常態分布怎麼幫助我們計算事件發生的機率，而更之前也看過了抽樣分布是如何形成常態分布的過程，現在就要利用這兩件事情來慢慢帶出什麼是統計學中的「假設檢定」了。