【金融知識】基金投顧說的平均獲利，你知道是哪種平均嗎？

有學過統計的人都知道，所謂的平均有許多不同的定義，我們今天要來學習在金融財務當中常見的平均方法。

這些平均方式可能是用在績效的結果，也可能是用在分析財務報表。

這些統計有時候差之毫釐、失之千里，我們在理解不同的統計分析跟看其結果時，不可不慎。

本篇文章簡單介紹5種平均數

1. 算術平均 Arithmetic mean
2. 幾何平均 Geometric mean
3. 調和平均數 Harmonic mean
4. 裁切平均數 Trimmed mean
5. 極端值調整平均數 Winsorized mean

這裡我們先提供一組原始數據(近20年0050季報酬率)。

並利用這組數據來演算各種平均數的結果，並比較差距。

算術平均 Arithmetic mean

算術平均，是我們日常生活中最常見的平均方法，就是從國小就開始教的那種平均方式。

就是把N個數字全部加起來除以N(對！就是這麼簡單的那種~~)。

算術平均很常出現在一般統計計算，但卻不常出現在我們計算投資報酬率。

現在，讓我們依據上面的統計數據來計算2004~2023年的算術平均報酬率。

Arithmetic mean = ( 5.62% + 5.67% + 12.68% + 6.41% - 46.51% + 71.74% + 8.77% - 18.88% + 8.01% + 9.11% + 13.88% - 9.12% + 18.19% + 14.42% - 8.09% + 28.41% + 26.04% + 19.07% - 24.26% + 22.87% ) ÷ 20

= 164.01% ÷ 20

= 8.2 %

經過簡單計算我們可以得知2004~2023年的算術平均報酬率為8.2%

幾何平均 Geometric mean

幾何平均其實是我們在計算報酬率當中，最重要的計算方式。

如果投資者從最一開始投放資金到最後都沒有取出資金或是新增加資金，也沒有更換投資標的的話，就適用幾何平均！

幾何平均公式如下：

當然，如果在各種不同時間點有買賣，或是資金的大小忽大忽小，那計算報酬率的方法就不能使用單純的幾何平均，而是要考慮「時間加權平均」或是「資金加權平均」，詳細計算可以參考以下這篇文章！

幾何平均就是把所有報酬率相乘之後再開根號。

只是報酬率需要先進行轉換，因為幾何平均「不能接受負數(小於0的數值)」。

我們先將各年度的報酬率都加上100%，可以得到新的一組數據如圖。

將各年度(轉換後)報酬率相乘再開根號可以得到 105.56%，算出來的結果需要扣除100%才是我們要的答案。

經過計算我們可以得知2004~2023年的幾何平均報酬率為5.56%

這個數值就是大家常聽到的「年化報酬率」，只不過這個數值【並沒有】校正除權息，所以並不是真正的年化報酬率。

但算到這裡已經可以看出來，使用『算術平均數(8.2%)』跟『幾何平均數(5.56%)』已經有不小的差距了！

調和平均數 Harmonic mean

這裡要一個比較困難的平均方式「調和平均數」，不過其實我們日常生活也滿常用的。

讓我們先思考一個國中的數學問題！

小K開車從台北要去高雄度假，「前半段時速120公里」，「後半段時速60公里」，前半段與後半段的距離相同，請問平均速率為多少呢？

如果你把 (120+60) ÷ 2 = 90 公里/小時，那很明顯的就錯囉！讓我們繼續看下去。

調和平均數的算法其實就是把所有數都先將其倒數，將這些倒數進行算術平均數，接著再進行一次倒數，其公式如下：

讓我們再回到剛剛的平均速率問題，因為時速快的時候所用的時間比較少，時速慢的時候所用的時間比較多，因此不能直接給予平均，所以這樣類型的題目要使用調和平均數來計算。

可以得出

2 /（（1/120）+（1/60））= 80 ，所以平均速率為每小時80公里。

如果，我們要使用調和平均數來計算上面的投資報酬率的話(雖然不適合)，可以使用轉換過的報酬率，因為調和平均數在這種情況下不適合負數，也不能有數字為『0』。

經過計算得出調和平均數為102.567%，扣除100%後可以得到2.567%。

到這裡我們介紹了三種常見的平均數計算方法「算術平均數」、「幾何平均數」、「調和平均數」。

關於這三種平均數，這裡有一個重要的觀念：

「算術平均數」>「幾何平均數」>「調和平均數」

裁切平均數 Trimmed mean (或稱切尾平均值)

接下來我們要來介紹最常被操弄的平均數之一「裁切平均數 Trimmed mean」！

在一般做統計的時候，常常會遇到的情況就是不小心就會有極端值。

(可能是有亂填數字的、不小心填錯的...等等。)

這時候該怎麼辦呢？

其中一種方式就是將「最大的幾個數字」跟「最小的幾個數字」一起【裁切】掉！

就當他們不存在！！！

10% Trimmed mean 就是將最大及最小的10%數值裁切掉。

5% Trimmed mean 則是將最大及最小的5%數值裁切掉。

讓我們來看最一開始的資料，並計算5% Trimmed mean(因為有20筆資料所以等於裁切掉最大跟最小的1筆數值)。

根據數據，我們裁切掉最差的2008年-46.51%以及最好的2009年71.74%來進行計算。

5% Trimmed mean = ( 5.62% + 5.67% + 12.68% + 6.41% + 8.77% - 18.88% + 8.01% + 9.11% + 13.88% - 9.12% + 18.19% + 14.42% - 8.09% + 28.41% + 26.04% + 19.07% - 24.26% + 22.87% ) ÷ 18

= 138.79% ÷ 18

= 7.71 %

跟一般的算術平均數8.2%相比少了0.49%。

聰明的你肯定想到，如果刻意刪除2008年但是保留2009年的績效，肯定會大幅提升整體績效，這雖然不是Trimmed mean但是卻是妥妥的資料選擇偏誤(Data selecting bias)，也是很多基金在推銷的時候會使用的手法。

極端值調整平均數 Winsorized mean

這種平均數跟「裁切平均數 Trimmed mean」有點像，一樣要將最大值跟最小值刪除掉，不同的地方是要用第二大跟第二小的數值來代替原本被刪掉的數值。

(或者用前N%跟後N%的平均數來代替該數值)

讓我們再一次用前面的案例來舉例：

我們先將0050近20年的投資報酬率由大到小排列：

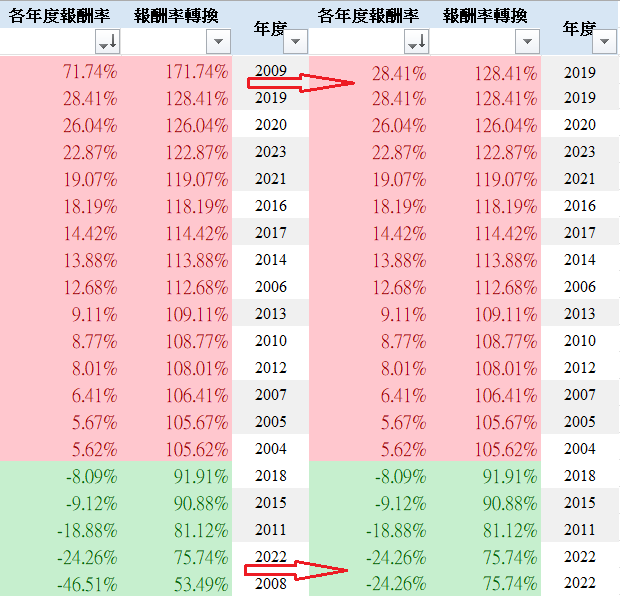
接著，讓我們用第二差(2022年)的數值來代替最差的(2008年)數值，用第二好的數值(2019年)來替換最好的數值(2009年)，如上圖右。

Winsorized mean = ( 28.41% + 28.41% + 26.04% + 22.87% + 19.07% + 18.19% + 14.42% + 13.88% + 12.68% + 9.11% + 8.77% + 8.01% + 6.41% + 5.67% + 5.62% - 8.09% - 9.12% - 18.88% - 24.26% - 24.26% ) ÷ 20

= 142.94% ÷ 20

= 7.14 %

經過計算可得極端值調整平均數為7.14%

後記：

我寫這篇文章的時候，特別跑去問隔壁的同事：「如果投資第一年賺3%、第二年4%、第三年5%，那你這三年的年化報酬率是多少？」

他想了一下下(大約10秒)，露出我這題肯定有陷阱的眼神，回答說：「4%！！」

今天如果你有耐心讀完這篇文章，就換我來問你一樣的問題，換你來解答囉！

如果你是要計算真正的投資報酬率，必須要考慮「時間加權平均」或是「資金加權平均」，詳細計算可以參考以下這篇文章！

💵如果喜歡我的文章，請大方按下愛心當作鼓勵💖

💵想要持續獲得金融財務知識，歡迎追蹤+分享💖

💵普及正確系統性的金融知識是我的志向，歡迎留言給我鼓勵💖