多層次模型中的 Random intercepts model with level-1 predictor 是層級 1 預測變量預測層級 1 結果變量的模型。本文將介紹該模型的一般方程式,並實際用R語言進行分析。最後介紹ML和REML估計法選擇。
公式
Random intercepts model with level-1 predictor 模型是一種具有隨機截距的多層次分析模型。假設第二層是學校,第一層是學生。Y是學生的數學成績,層級 1 預測變量為固定效果,代表層級 1 預測變量對結果變量的影響被限制為相同的固定值,不會隨著學校不同而不同;層級 1 截距(β0)為隨機效果,代表β0隨著學校不同而不同。數學公式可以表示如下:
Level 1:
層級 1 結果變量 = β0 + β1 * 層級 1 預測變量 + e
Level 2:
β0 = β00 + e00
β1 = β10
Combined:
層級 1 結果變量 = β00 + β10 * 層級 1 預測變量 + e00 + e
其中:
- β00 是層級 2截距,表示當層級 2 預測變量的斜率(β1 )為0時,所有群組的層級 1 結果變量的平均值。固定效果。
- β1 是層級 1預測變項的斜率係數,表示層級 1 預測變量在層級 1 結果變量中每增加一個單位時的平均變化。固定效果。
- e00 是層級 2截距的隨機效應,表示層級 2群組間截距的變異量。隨機效果。
- e 是residual,層級 1變異量。隨機效果。
- β10 是學校級斜率的總平均值。
- e 是residual,層級 1變異量。
- e 和e00 必須是不相關的才符合前提假設
- e 和e00 必須是常態分配才符合前提假設
- 如下圖,截距具有隨機效果就是認為截距會因為學校不同而有變化,所以每條線起點有差異。
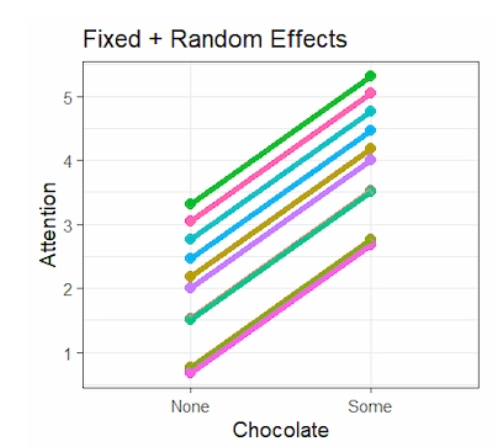
範例
# 載入相關套件
library(lme4)
lme4 套件提供了多層次分析的函數。
# 生成數據
set.seed(1234)
# 層級 1 結果變量
math_score <- rnorm(1000, mean = 50, sd = 10)
# 層級 1 預測變量
ses <- rnorm(1000, mean = 50, sd = 10)
# 學校ID
school_ID <- rnorm(100, mean = 50, sd = 10)
# 合併數據
df <- data.frame(math_score, ses, school_ID)
set.seed() 函數用於設定隨機數生成器的種子,以便可以重複生成相同的數據。rnorm() 函數用於生成常態分布的隨機數。以下是這三個變量的介紹:
層級 1 結果變量
- 名稱:math_score
- 描述:學生的數學成績
- 層級:1
- 值:從常態分佈中隨機抽取1000,平均值為 50,標準差為 10
層級 1 預測變量
- 名稱:ses
- 描述:學生的社會經濟地位
- 層級:1
- 值:從常態分佈中隨機抽取1000,平均值為 50,標準差為 10
學校 ID
- 名稱:school_ID
- 描述:學生所屬的學校
- 層級:2
- 值:從常態分佈中隨機抽取100,平均值為 50,標準差為 10
data.frame() 函數用於將數據合併到一個數據框中。數據內容如下:
math_score ses school_ID
1 37.92934 37.94667 40.26181
2 52.77429 53.01467 49.00369
3 60.84441 34.60855 48.89265
4 26.54302 56.35371 61.92195
5 54.29125 57.02952 33.44114
6 55.06056 30.94117 39.54357
7 44.25260 59.38921 32.59761
8 44.53368 47.75508 55.13121
9 44.35548 43.26183 45.54043
10 41.09962 54.45787 31.60806
11 45.22807 62.80617 41.80152
12 40.01614 65.65130 40.04790
13 42.23746 37.99454 52.97310
14 50.64459 45.62305 55.57416
15 59.59494 51.46381 37.26663
16 48.89715 50.66019 60.25073
17 44.88990 45.54964 54.66612
18 40.88805 26.57888 52.33918
19 41.62828 47.21618 52.64442
20 74.15835 38.18196 54.32420
# 跑模型
model <- lmer(math_score ~ ses + (1|school_ID), data = df)
lmer()函數用於運行多層次線性混合效應模型。- 若不想使用REML估計法可以改用ML估計法:
lmer(前面一樣..., REML = F) math_score是結果變量。ses是預測變量。(1|school_ID)表示模型包括一個隨機截距,採用school_IDdata = df表示模型將在df數據中使用。summary(model)函數用於顯示模型的結果。
以下是模型的結果:
Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: math_score ~ ses + (1 | school_ID)
Data: df
REML criterion at convergence: 7439
Scaled residuals:
Min 1Q Median 3Q Max
-3.3188 -0.6397 -0.0229 0.6457 3.2576
Random effects:
Groups Name Variance Std.Dev.
school_ID (Intercept) 0.00 0.000
Residual 99.25 9.962
Number of obs: 1000, groups: school_ID, 100
Fixed effects:
Estimate Std. Error df t value Pr(>|t|)
(Intercept) 46.84758 1.64136 998.00000 28.542 <2e-16 ***
ses 0.05756 0.03212 998.00000 1.792 0.0735 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
解釋
Formula行顯示模型的公式。Random effects:Residual= 99.25 = e = 殘差Random effects:school_ID (Intercept)= 0.00 = e00 =截距的隨機效果,它表示每所學校的平均數學成績與總平均值之間的差異。Fixed effects: (Intercept)= 46.84758 = β00 = 學校的數學總平均值Fixed effects: ses= 0.05756 = β1 = β10 =社會經濟地位的斜率
結論
模型的結果表明,截距的隨機效果並不顯著,可以考慮將截距改為固定效果。社會經濟地位與數學成績之間為不顯著的正向關係。根據斜率表示,每增加一個單位的社會經濟地位,數學成績預計會增加 0.05756 個單位。但因為p值並未達到顯著水準,所以代表該斜率係數 = 0。

















