服用須知 : 本系列內容力求白話、通順、易懂(畢竟是筆記嘛😂),因此較沒有極度嚴謹的數學證明,如有特別嚴謹的需求還是要參考教科書!
知識基礎 :
在正式進入梯度的主題之前,我先帶各位複習一下大一微積分的偏微分符號及其意義 :
- 𝒹ƒ : ƒ值的微小增量,同理適用於𝒹x、𝒹y等......
- ∂ƒ/∂x : ƒ在x方向上的偏微分(變化率),同理適用於∂ƒ/∂y等......
- i、j、k:單位向量
場變化增量:
假設有一坐標空間,內部充斥一個「場」,是甚麼場我們先不管,只知道這個場的強弱分佈依循ƒ關係式。
空間中有一個點,將其沿著一段微小的向量𝒹𝓁移動(如圖),這段位移增量可以表示成x、y、z三個方向分量的相加,亦即:𝒹𝓁=i𝒹x+j𝒹y+k𝒹z。
再來,我們想知道這個點移動前後,ƒ的值改變了多少(即𝒹ƒ),已知xyz三個方向的移動都會分別影響ƒ的值,於是拆開來分析:
- ƒ在x方向上的改變=ƒ在x方向上的變化率×點在x方向上的移動量,亦即:

- ƒ在y、z方向上的改變量,同理可得。
記得把各方向上的變化量乘上單位向量ijk,使其具有方向性,接著把他們相加起來不就是𝒹ƒ了嗎?因此移動後ƒ的增量為:

梯度運算子(Del operator) :
所謂運算子(operator),就是像一部機器,輸入一個值就會輸出相對應的結果。今天設定一個運算子 ∇ ,定義:

以輸入ƒ為例,則∇ƒ為f的梯度(念作Gradient f,簡寫為grad f):

拿剛剛的∇ƒ和之前提到的動點移動路徑向量𝒹𝓁(=i𝒹x+j𝒹y+k𝒹z)做內積,會發現居然得到了場變化增量𝒹ƒ(注意,內積過後是純量),亦即:

梯度(Gradient)的意義:
由上式可以看到梯度的定義漸趨明朗(梯度和路徑的內積=場值變化量),如果說,∇ƒ向量和𝒹𝓁向量間有夾角θ,則可將上式改寫為:

當cosθ=1(θ=0度),會發現場變化增量有最大值。
👉意義1:位移向量和梯度向量同向時,場值的變化量最大。因此梯度的方向就是最大變化率的方向。
然而,要達到最大場值變化的路徑有百百種,就如同一座山丘,從底部到山頂的路徑有很多種,我們要找最短的位移𝒹𝓁,但因為路徑最短,所以路途會最陡,ƒ的變化率最大,但增量是一樣的。
想要最短距離達成最大效益,想當然θ要先=0度,也就是移動方向已經對準最陡峭的向量了,此時ƒ的變化率正是梯度∇ƒ(因為增量=變化率乘位移)。
👉意義2:沿著梯度方向走,在梯度最大值處,可最快達到最大增量。
把數學式移項,得到:
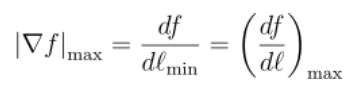
可見梯度最大值,ƒ隨路徑的變化率也最大。
👉意義3:梯度就是隨不同路徑移動時,ƒ增量的變化率。
參考資料:
中山大學開放式課程 電磁學 周啟教授
周啟電磁學網路課程講義 第一章向量算符
以上就是我的筆記,由於內容屬於原創,如上述有用詞不精、詞不達意、或是觀念錯誤等情況,麻煩在底下留言告知,我會加以修改,請各位多多指教了🙇♀️!
📍更多實用資訊,歡迎關注理工女子的宿舍漫遊(IG&Vocus)
















