我們在 Day 4 時花了大量篇幅講解 Shapley Value 的四大特性:效率性、對稱性、虛擬玩家零收益、可加性。今天要反過來證明說,如果有個效益分配函數(對每個賽局 v 都指定一個效益分配向量)

滿足這四個特性的話,則這個 f 必定就是 Shapley Value
四大特性簡要回顧
效率性 Efficiency
Shapley value 滿足

代表整個博弈的總價值 v(N) 會被完整地分配給所有玩家,沒有浪費或剩餘。
對稱性 Symmetry
對稱性:若對於任何不包含玩家 i 與 j 的聯盟 C⊆N,皆有
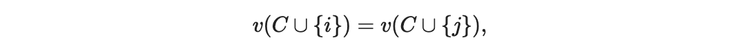
則稱玩家 i 與 j 在此博弈中「對稱」。也就是說,不論在哪個子集合 C 裡,將 i 加入或將 j 加入,其貢獻都一模一樣。
對於兩個對稱的玩家 i 與 j ,Shapley value 必定會分配給他們一樣的效益
虛擬玩家零收益
沒貢獻的玩家:若對於任何不包含 i 的聯盟 C⊆N,都有
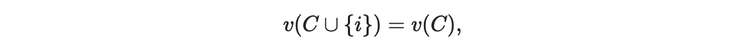
則稱玩家 i 為 Dummy Player (沒貢獻的玩家)。
Shapley value 必定不會分配給 Dummy Player 任何效益
可加性 Additivity
令 v1 與 v2 為兩個賽局,則 Shapley Value 滿足

以上四個重要特性,詳細證明請見 Day 4 的文章
從線性空間的結構來證明唯一性
根據昨天的結論,我們知道每個賽局都可以寫成

而其中 u_T(S) 叫做齊一性賽局(Unanimity games):給定任意非空子集 T ⊆ N, unanimity game 的定義如下:

也就是只有當集合 S 包含整個集合 T 時,其效用才為 1,否則為 0。
我們現在假設

滿足上面那一小節的四個特性,並證明他就是 Shapley Value。
證明
因為 f 是可加的(Additive),所以

於是只要證明到對於所有非空子集 T 都有

那就證明完畢了。
好現在我們就認真證明這個等式

對於 i ∈ N - T ,我們知道對於所有聯盟 S

因此根據虛擬玩家零收益的特性,我們可以寫出

對於 i, j ∈ T ,首先注意到對 u_T 來講,這兩個玩家是對稱的,因為

其中

以及同樣的

因此我們知道

同樣的論證對所有的 i, j ∈ T 都有效,於是就可以寫下

最後,使用效率性

而左式可以寫為

但是因為 (1) 所以

而正好根據 Shapley Value 的定義

於是我們就完成了證明。
Takeaway
Shapley Value 的四大特性(效率性、對稱性、虛擬玩家零收益、可加性),其實正好也可以是 Shapley Value 的定義。
Reference
Branzei, Rodica, Dinko Dimitrov, and Stef Tijs. _Models in cooperative game theory_. Vol. 556. Springer Science & Business Media, 2008.














