基本觀念
什麼是有理函數
有理函數是指形如:

我們的目標是將這樣的函數用部分分式(Partial Fractions)的方式拆解,進而對每項積分。
使用條件
- 條件 1:是「有理函數」
- 條件 2:分子次數 < 分母次數
- 若不是,要先做「多項式長除法或者使用綜合除法」。
- 最後根據分母的因式類型分類:
部分分式拆解的基本類型
- 線性因式(不重根)

- 線性因式(重根)
例如:

- 二次不可約因式
例如:

這裡:
- x2+1 是不可約二次因式
- x−2 是線性一次因式
所以應該拆解為:

範例1

分母分解:

部分分式形式:

兩邊同乘分母:

整理後使用比較法或代入法求 A,B,本題使用帶入法:

再來就很好積分了:

範例2
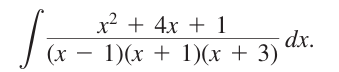
設:

兩邊同乘分母:

若使用比較法,需要展開右邊所有項:

全部展開相加:

建立聯立方程式:

經過漫長計算後你會得到:

整理後積分式:

範例3

設:

兩邊同乘分母:

展開右邊:

比較左右兩邊係數得到係數A、B後,帶回積分式:

逐項積分:

範例4

利用長除法或綜合除法:

再將 x2−2x−3 因式分解:

設部分分式(對餘式部分):

最後找到係數後,整理為積分形式:

積分每一項:

範例5

整體設為:

兩邊同乘分母後得到:

等於:

比較左右兩邊係數後得到A、B、C、D,帶入積分式:

分項積分:

計算出最終答案:

求係數的其他方法
使用「Heaviside 快速法」解出每個係數
這種方法只適用於分母全為一次不重根因式的情況,且形式是:

那麼:

例如:

使用 「differentiating」 找出係數
例如:

兩邊同乘分母

代入 x=−1,可得 C=−2。
接下來,對兩邊微分,得:

再微分一次,得到:

最終結果為:

本頻道持續更新中(內容涵蓋前端程式設計入門、大學必備程式設計入門、電子系專業課程入門、數學微積分題解)如果身旁有相關科系的學生,不妨推薦一下喔~
相信這裡會是家教或線上課程之外,高中、大學生系統性綜合學習的好選擇。
最後感謝您的觀看!












