【GIS】幾乎每天在用地圖，你是否知道電子地圖是由那些元素組成?什麼是點、線、面?

一般來說，地圖會至少由以下3個元素組成，分別是:

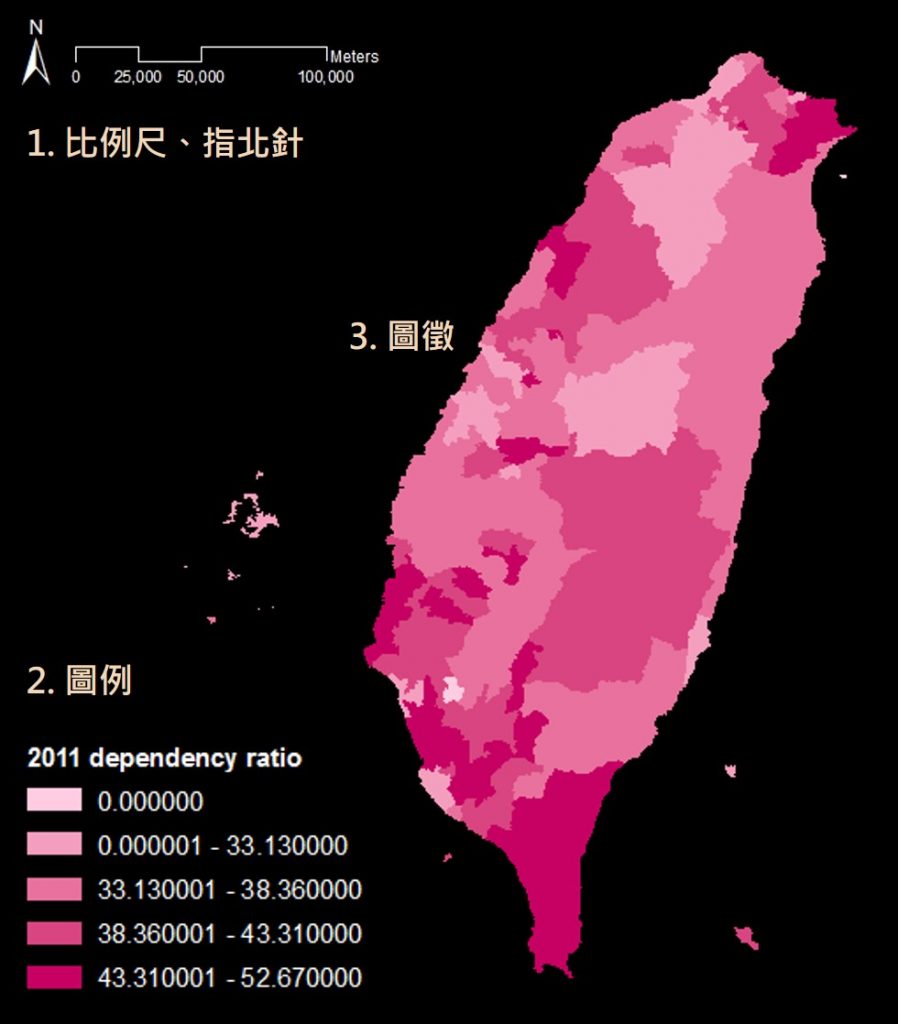
(一) 比例尺、指北針

比例尺用來說明圖上尺寸與真實世界的比例，如果可以的話，建議比例尺的數字是比較好閱讀的整數，例如1:100、1:5000等，不難想像如果是1:62548會有多難閱讀。指北針的話其實可標可不標，不標的話通常就是以正上方為正北。

(二) 圖例 (legend)

因為地圖可以用顏色、大小、線段粗細等等多種方式來做資料視覺化(data visualization)，所以圖例應該要讓讀者不需要地圖作者解釋也能讀懂地圖上的資料。

(三) 圖徵 (feature)

圖徵是地圖上的靈魂元素，在GIS中通常會對應到向量(Vector)的圖徵(Feature)，通常會有點(point)、線(line)、面(polygon)三種形式；而在GIS(地理資訊系統)領域裡，以上3種圖徵都是向量(vector)資料的範圍，GIS領域中常見的資料類型另外還有網格(raster)，本篇文章將聚焦在向量資料。

前面提到圖徵是地圖的靈魂元素，而常見類型有點、線、面三種。地圖上通常會用不同類型的圖徵來代表真實世界的資料。

我們知道，一組(x,y)座標代表一個點；2個點可以連成一條線；而最少3條線就可以形成一個面。所以這三種圖徵的基本組成都是(x,y)座標，點就是一組座標，線就是兩個座標，面就會有很多座標。

而全世界人都在用的座標系統就是經緯度，所以，真實世界上的地貌、現象、活動...等很多都可以用座標來呈現在地圖上。。

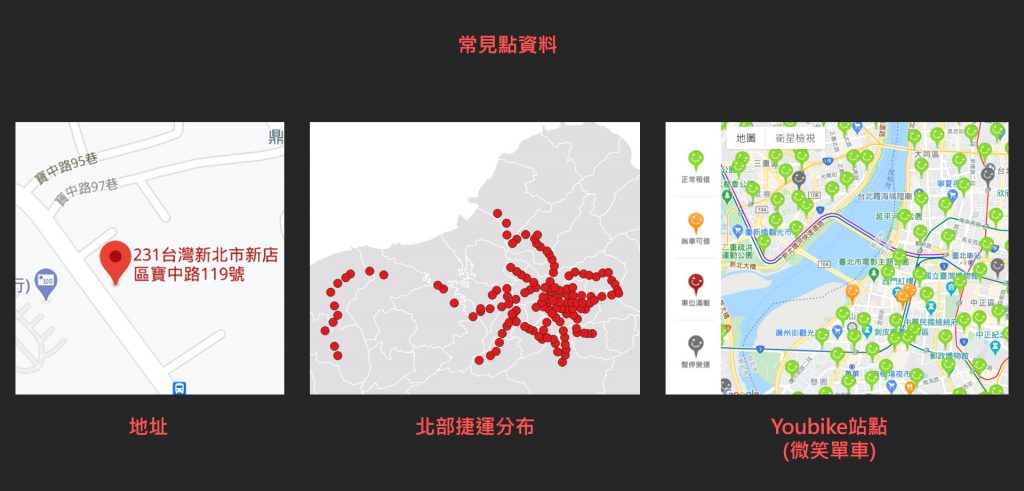
(一) 點圖徵(point feature)

點圖徵最常用來表示站點類的資料，舉凡公車站、捷運站、火車站通常都會以點圖徵來表示。另外我們也常用點來表示一個地址的位置。

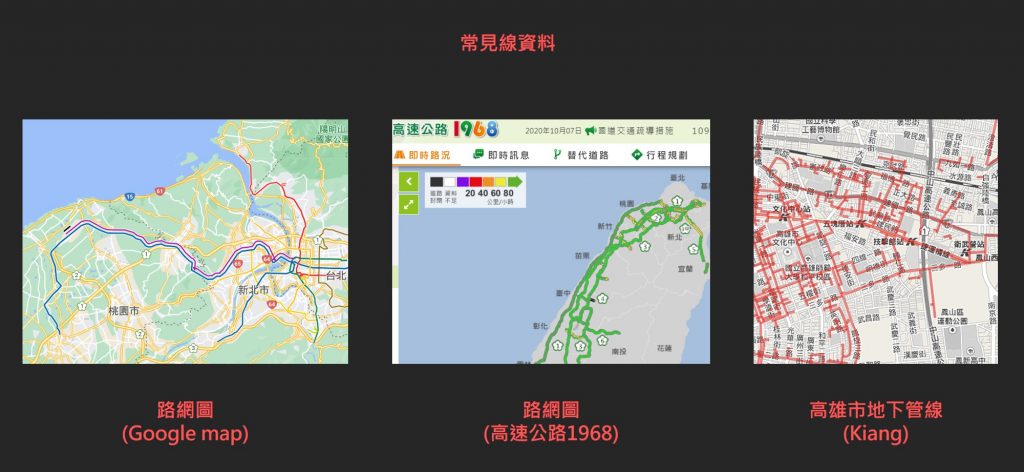
(二) 線圖徵(line feature)

線圖徵最常對應到兩類資料，第一種是道路、路線；第二種則是管線類的資料。雖然道路有寬有細，甚至同一條路裡面還有區分車道、分隔島等等，但是依據使用情境不同，通常是以線圖徵來表示道路就可以滿足需求。

(三) 面圖徵(polygon feature)

各種不同尺度的土地範圍都可以用面圖徵來表示，小至一棟房子、一個社區；大至縣市、國家等都適合用面圖徵來表示。

而下圖中的土地範圍則是都市計畫領域時常看見的圖，它其實跟你我的生活息息相關，不同顏色代表不同的土地使用規範，這些規範也會影響建物能蓋多高、能不能開店、能開甚麼店...等。這些都有賴面圖徵來呈現。

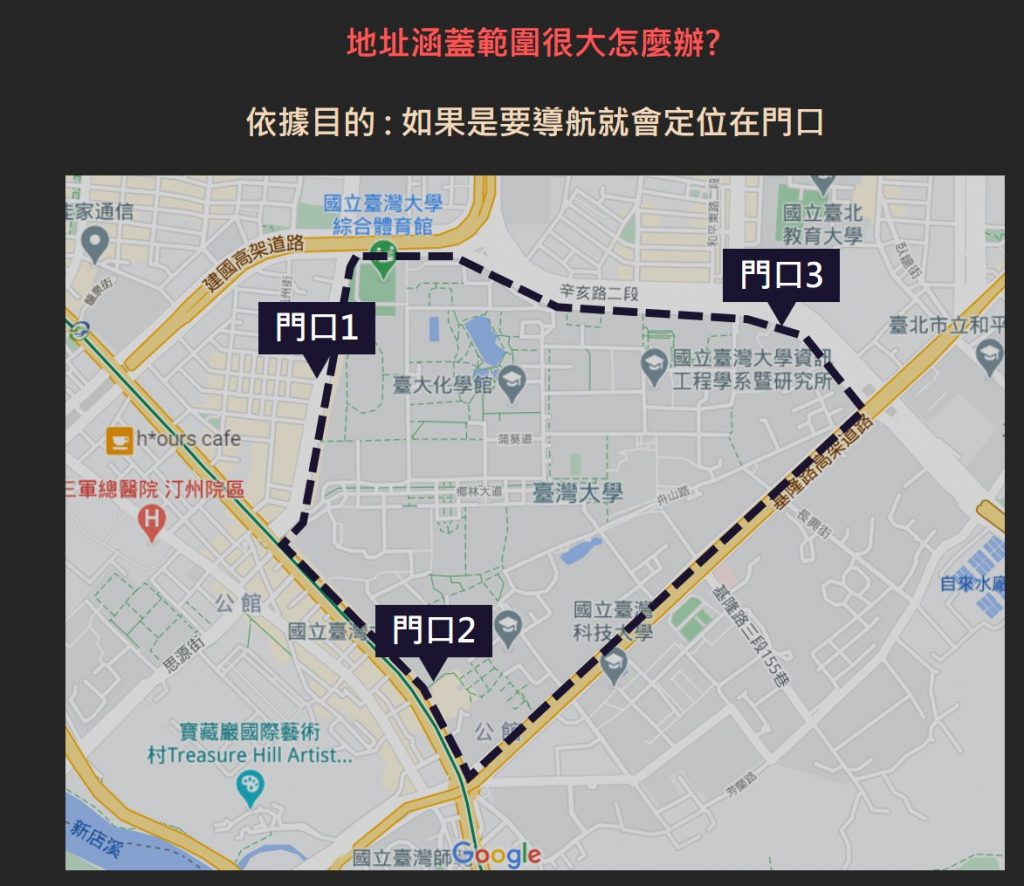
前面有提到地址常用一個點來代表，但地址指的是一棟建物或是一大片土地的範圍，為什麼可以只用一個點來代表呢?通常地址的功用是讓人找到這個地方，也就是拿來導航，所以用一個點來代表是足夠的。

但是如果這個地址是代表很大的一個範圍呢?例如大學範圍這麼大，也只用一個地址代表?這時候就要看目的了，如果目的是導航的話，通常就會把所有門口(導航應該都會把人導到門口吧)都用點標示出來。

本文同步刊載於我的個人網站：鍾肯尼的雜記。