假設你是一位管理全球股票投資組合的投資經理人,基礎做法通常是:
- 使用歷史資料 來估計各個市場或產業的平均報酬與風險(標準差)。
- 將這些平均報酬視為「輸入參數」,然後套用馬可維茲均異化模型(Markowitz Mean-Variance Model or Mean-Variance Optimization)來決定最適投資組合。
但在現實中,歷史資料的估計不僅受到區間選擇的影響,更可能因為未來不一定重複過去的走勢,而導致投資組合對輸入參數的微小變動極度敏感:
- 只要稍微改變某個市場的報酬預測,投資組合的權重就可能劇烈搖擺。
- 加上你作為投資經理人,其實對未來趨勢(例如「美國科技股將比歐洲傳統產業成長更快」)有某些主觀判斷,但傳統模型難以「系統化」地把你的主觀觀點納入。
這時 Black-Litterman Model 就能派上用場。它先假設「若市場達到均衡,則各資產的權重應與其市場總市值的比例相符」,並推導出一組隱含的均衡報酬。接著,你可以把自己對「美國科技股」或「歐洲市場」等的看法,以「主觀觀點」的方式輸入模型,並對自己的觀點設定「信心程度」。Black-Litterman Model 會在考量整體市場均衡的基礎上,將你的觀點適度融入,最後輸出一個更穩定且能反映你看法的投資組合。
為什麼這很重要?
- 在真實世界中,僅憑歷史平均報酬去做投資決策常有偏誤。
- 你可以系統化地將「主觀看法」結合「市場均衡」,而非純粹依賴個人直覺。
- 相較於傳統方法,Black-Litterman Model 的投資組合結果更「穩定」,極端配置現象較少。
Black-Litterman Model 的精隨
- 市場均衡(Market Equilibrium)
- 該模型在起點認定,如果所有投資人都是理性的,且市場達到供需均衡,則各資產的最適權重等同於它們在市場中的市值比例。藉由反推出「隱含的均衡期望報酬」,給出一個不會過度依賴歷史資料或投資人情緒的「基準觀點」。
- 主觀觀點(Views)與可信度(Confidence)
- 投資人可以表達對某些資產或市場的看法,例如「A 產業的未來報酬率將高於均值 2%」,並給定一個「信心程度」。這些觀點與市場均衡相結合時,形成更客觀的投資組合調整依據。
- 貝葉斯更新(Bayesian Update)
- Black-Litterman Model 透過貝葉斯方法來融合「市場隱含的均衡報酬」和「投資人主觀看法」。信心程度越高,模型調整權重就越朝投資人觀點傾斜;信心程度越低,就越保留市場均衡的結果。最終得到的期望報酬矩陣與投資組合權重更具彈性與穩定性。
- 更穩定、直覺且可控的結果
- 避免了傳統均異化模型可能出現的「輸入輕微波動就導致權重大幅搖擺」的情況。
- 藉由控制「主觀觀點」的強弱,投資人不需要“無條件”相信模型或個人看法,而是能在兩者之間找到平衡。
模型建構
在傳統 Markowitz 的MVO架構下,我們希望找出能最大化投資組合效用(Utility)的權重向量 w。若有 N檔資產,其期望超額報酬(相較於無風險利率)向量為 μ,資產報酬的協方差矩陣為 Σ,投資人對風險的厭惡程度(Risk Aversion Coefficient)為 λ,則常見的投資組合效用函數可寫作:

對上式取一階導數並令其為零,可得:

此即傳統平均-變異模型下的最佳權重解。
隱含市場平衡報酬(Implied Equilibrium Return)
Black-Litterman 模型的第一步是透過「反向優化」(Reverse Optimization),將市場權重視為「平衡權重」w_m:假設市場目前的權重即為最適解。則從上式可得市場均衡之「隱含期望超額報酬」μ_eq為:

其中:
- w_m 為 N×1 的市場權重向量(例如市值加權指數的權重)。
- λ為風險厭惡係數,可由歷史市場風險溢酬(market risk premium)及波動度推得,通常介於 2~4 之間。(若以美股歷史平均超額報酬約 6%、波動度約 15% 為依據,則λ = 0.06/0.15^2≈2.7)
納入不確定性調整係數 τ
Black-Litterman 模型中,將市場隱含期望報酬 μ_eq視為「先驗分佈」(Prior),並假設 μ_eq與協方差矩陣 Σ 同為常態分佈。但因「期望報酬本身的變動」通常遠小於「單期報酬的變動」,我們常在 Σ 前乘上一個「風險調整倍數」τ,使得先驗對 μ_eq 的不確定度更小一些。常見的 τ 值介於 0.01~0.05 之間,或依據樣本期間 T 反推 τ≈1/T
若將歷史 T 期的平均報酬視為「期望報酬的估計」,其標準誤差約為樣本標準差的1/√T。因此在 Black-Litterman 架構下,可將 Σ 的量級縮小約一個 1/T的倍數,即 τ=1/T。
設定主觀觀點與其不確定度 Ω
Black-Litterman 模型的核心在於,投資人可對部分資產或組合提出「觀點」,並賦予「觀點不確定度」Ω(即該觀點的信賴區間)。假設總共有 K 條觀點,則可用下列線性方程式表示:
Q = P μ + ε
其中:
- Q為 K×1的觀點向量,表示每條觀點對應的「預期報酬」。
- P為 K×N的配置矩陣(每條觀點如何加總到各資產)。
- μ為我們想要推估的資產期望超額報酬(也是 Black-Litterman 中的「未知量」)。
- ε 表示觀點的誤差項,其協方差矩陣為 Ω(對觀點的置信程度越高,Ω越小)。
例如,假設有 5 檔股票:
- 股票 1、2:屬於「非必需消費品(consumer discretionary)」產業,其相對市值比重各 0.5 與 0.5。
- 股票 3、4、5:屬於「消費必需(consumer staples)」產業,市值比重依序為 0.5、0.3、0.2。
投資人根據研究得到 3 條觀點:
- 單一股票觀點:股票 3 的期望報酬為 10%,估計誤差波動度為 10%。
- 產業相對觀點:非必需消費品(加權 0.5/0.5)將比消費必需(加權 0.5/0.3/0.2)多賺 3%,估計誤差波動度為 4%。
- 長/短組合觀點:一個總權重加總為 0 的投資組合 [+0.4, −0.6, −0.4, +0.4, +0.2],預期能賺 4%,估計誤差波動度為 3%。
此時可將 3 條觀點合併成(1 row 1 view):

若假設三條觀點之間互不相關,則其不確定度矩陣 Ω 為(波動度的)對角矩陣:

Black-Litterman 後驗報酬
若忽略推導過程,最終得到的 Black-Litterman 後驗報酬向量通常被寫成:

若投資人對觀點極度有信心,Ω很小,則後驗報酬會較接近觀點 Q。反之,若對觀點信心不足,Ω 大,後驗報酬會偏向市場隱含的 μeq。
(我們也可推導出更新後的報酬協方差,只是因 τ 很小,且加入觀點後常能進一步降低不確定性,因此實務操作時,Σ本身常被視為已相當接近後驗協方差。若模型對觀點有較高信心,後驗報酬分配的變異自然會小於原先市場隱含分配。)

重新優化投資組合
得到後驗期望報酬 μ^之後,我們可再次進行MVO,找出新權重 w^:

Ω 的估計方法
在 Black-Litterman 中,Ω(觀點的不確定度)是最具彈性、也是最抽象的部分。投資人可依不同觀點決定 Ω 的數值大小及各觀點之間的相關性(Ω 的對角線外元素)。
- 質化法(Qualitative Approach)
例如 Thomas Idzorek(2005)提出一種「根據信心水準」的直覺性做法。投資人僅需對每條觀點給出「0~100%」的信心,例如信心 100% 表示該觀點幾乎是「必然正確」。此法藉由一次次迭代,找出能使優化組合「最接近」該信心水準的 Ω對角元素。若兩條觀點之間有相關性,也可進一步對 Ω 的非對角元素進行設定。 - 量化法(Quantitative Approach)
若觀點來自量化因子模型或回測結果,我們可直接以「歷史上該觀點(因子)對超額報酬預測的協方差」作為 Ω。但由於 Ω 代表的是「對期望報酬」的變異,而非「對單期報酬」的變異,實務上常需乘上一個小於 1 的縮放係數(類似 τ 的概念),以反映「期望值的波動度遠小於單期報酬」。
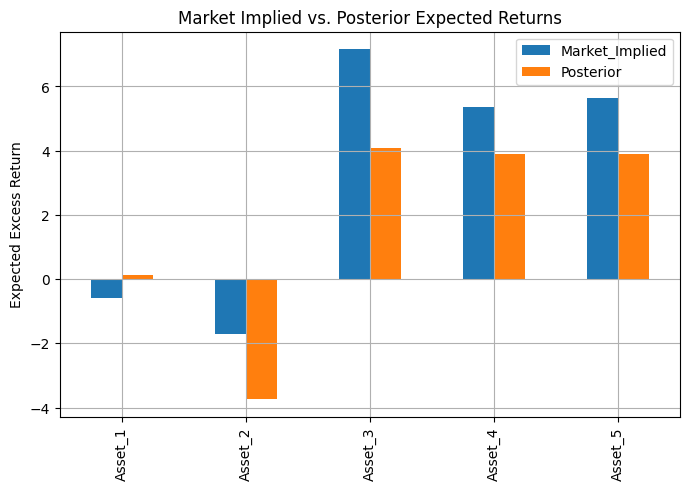
Python實際測試
以隨機數生成Covariance以及market weight


假設有 3 條觀點(K=3):
1. 看好資產 1,期望它相較於無風險利率的超額報酬為 8%
2. 認為資產 2 與 3 組合(各權重 0.5, 0.5),期望報酬有 6%
3. 資產 4 與 5 的 Long/Short 組合,(權重 1, -1),期望有 2%
可以得出Market implied return 以及Posterior expected returns
如果根據求解出之μ^,重新求解MVO























