AI說書 - 從0開始 - 52

我想要一天分享一點「LLM從底層堆疊的技術」，並且每篇文章長度控制在三分鐘以內，讓大家不會壓力太大，但是又能夠每天成長一點。

先用一張圖概括 Attention 機制的輸入與輸出：

Attention 機制縱覽

• 以一個句子包含四個字為例子
• a¹、a²、a³、a⁴ 是四個字各自對應的向量
• 每個向量可以是 Input Layer 輸入也可以是 Hidden Layer 輸出
• 這四個向量經過 Attention 機制會轉成向量 b¹、b²、b³、b⁴
• 我現在就是要來闡述 Attention 中間步驟

計算 Query 與 Key：

• 向量 a¹ 乘上矩陣 W^q 變成向量 q¹
• 向量 a² 乘上矩陣 W^k 變成向量 k²
• 向量 a³ 乘上矩陣 W^k 變成向量 k³
• 向量 a⁴ 乘上矩陣 W^k 變成向量 k⁴
• 向量 q¹ 乘上向量 k² 變成純量 a_1,2 ，以此類推得到 a_1,3 與 a_1,4

然後算 Attention Score：

• 向量 a¹ 乘上矩陣 W^k 變成向量 k¹
• 向量 q¹ 乘上向量 k¹ 變成純量 a_1,1
• 將手上有的 a_1,1、a_1,2、a_1,3、a_1,4 做正歸化得到 a^'_1,1、a^'_1,2、a^'_1,3、a^'_1,4

再來計算輸出：

• 向量 a¹ 乘上矩陣 W^v 變成向量 v¹
• 向量 a² 乘上矩陣 W^v 變成向量 v²
• 向量 a³ 乘上矩陣 W^v 變成向量 v³
• 向量 a⁴ 乘上矩陣 W^v 變成向量 v⁴
• 向量 v¹ 乘上 a^'_1,1 、 向量 v² 乘上 a^'_1,2、 向量 v³ 乘上 a^'_1,3 、 向量 v⁴ 乘上 a^'_1,4 ， 這四項相加得向量 b¹

同理可以計算 b² 、 b³ 、 b⁴ ，現在我要闡述矩陣做法：

• 向量 a¹ 乘上矩陣 W^q 變成向量 q¹ 、 向量 a² 乘上矩陣 W^q 變成向量 q² 、 向量 a³ 乘上矩陣 W^q 變成向量 q³ 、 向量 a⁴ 乘上矩陣 W^q 變成向量 q⁴ ，然後堆疊q¹ 、 q² 、 q³ 、 q⁴ 變成矩陣 Q
• 同理整理出矩陣 K 與矩陣 V

接著計算 Attention Score：

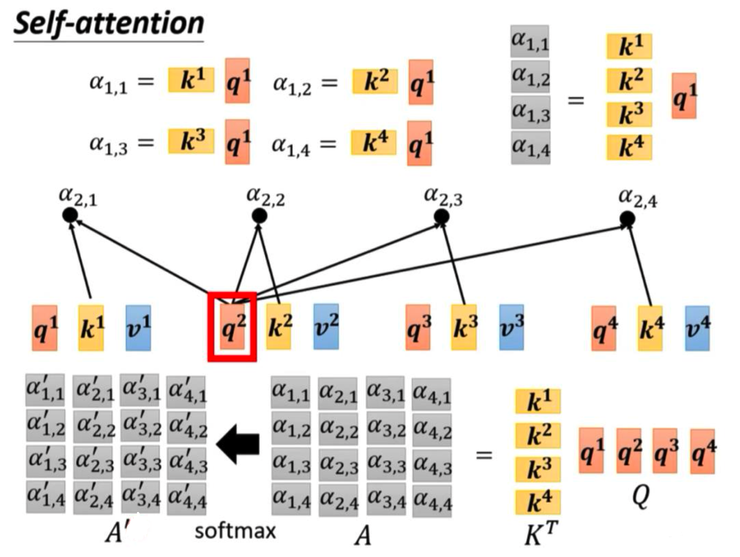
• 之前說向量 q¹ 乘上向量 k¹ 變成純量 a_1,1 、 向量 q¹ 乘上向量 k² 變成純量 a_1,2 、 向量 q¹ 乘上向量 k³ 變成純量 a_1,3 、 向量 q¹ 乘上向量 k⁴ 變成純量 a_1,4 ，這用矩陣來說就是：矩陣 K^T 乘上矩陣 Q 的第一欄變成矩陣 A 的第一欄
• 以此手法可以堆出整個矩陣 A
• 矩陣 A 執行正歸化即可得到矩陣 A^'

最後算輸出：

• 之前說向量 v¹ 乘上 a^'_1,1 、 向量 v² 乘上 a^'_1,2、 向量 v³ 乘上 a^'_1,3 、 向量 v⁴ 乘上 a^'_1,4 ， 這四項相加得向量 b¹
• 上述作法是矩陣 V 乘上矩陣 A^' 的第一欄，做堆疊之後就是矩陣 O 是矩陣 V 乘上矩陣 A^'

最後總整理為：

• 向量 a¹ 、 向量 a² 、 向量 a³ 、 向量 a⁴ 以欄為堆疊方向行成矩陣 I
• 矩陣 I 和矩陣 W^q 相乘得到矩陣 Q，同理得到矩陣 K 與矩陣 V
• 矩陣 K^T 乘上矩陣 Q 形成矩陣 A
• 矩陣 A 做正規化得到矩陣 A^'
• 矩陣 V 乘上矩陣 A^' 得到矩陣 O