Hi, 我又回來一下了。一週實習兩天、參加兩個社團還要修課,好累。
本篇文章將討論最佳槓桿率涉及報酬與波動耗損的取捨,這是非常數學的問題,因此勢必需要引用大量數學來證明,若讀者想要略過數學上的操作,文章後半段也有美國股、債、黃金的實證資料可進行參考。
首先最簡單的,我們考慮原型指數經過了三天的漲跌最終回到平盤,第二個案例相對於第一個案例的波動性更高。

波動較低

波動較高
簡單的實驗發現0.5倍槓桿經過三天的漲跌最終淨值比期初還要來得高,波動耗損變成了「波動利益」,反觀2倍以及3倍槓桿就沒有那麼好運了,它們承擔了大家所說的「波動耗損」,隨著波動的程度越大,波動利益以及波動耗損的影響來得更加劇烈。
我們得出一個簡單的結論是:「市場平盤的狀況,小於一倍的槓桿可以得到波動利益,大於一倍的槓桿反而會得到波動耗損。」這個結論相當重要,理解這個結論後就可以間接地理解為什麼多資產槓桿經常會比單資產槓桿還要來得更好。
市場上漲的狀況下呢?我們就會需要精細地計算槓桿帶來的報酬和與之相伴地波動耗損孰高孰低,以下開始利用數學介紹四種計算最佳槓桿率的方式,文末我們將對股票、債券、黃金進行實證。
一、凱莉公式
凱莉公式的證明相當簡易,它選擇極大化幾何報酬率。
令勝率為p、賠率為b、下注比例為f。我們可以將資產淨值V整理成下式。

令左式為G,右式的部分根據大數法則W/T會收斂至P,將式子整理如下。

接下來只需要將G對f求微分後就可以得到最適的下注比例f。

這個方法雖然簡單但相較期望值、變異數不直觀,所以我不太喜歡這個公式。
二、泰勒展開幾何報酬率
這個方法選擇極大化期望單期對數報酬率,這是因為單期對數報酬率相加正好是總對數報酬率。
令R為單期對數報酬率,可以得到以下近似公式 R - 1/2*R^2。

接下來僅需要將左右兩式取期望值,即可得到期望單期對數報酬率的近似公式。又因為槓桿K倍會放大算術平均報酬率K倍和變異數K平方倍,因此我們就可以得到槓桿報酬率(G),將G對k微分後即可得到最佳槓桿率k。

三、幾何布朗運動
隨機微積分非常艱澀,這部分我選擇跳過了前面步驟的介紹,證明過程較不嚴謹。
當假設股價遵循幾何布朗運動且單期報酬率為常態分布時,對數股價就會是對數常態分配,如下式。

接下來透過一些簡單的運算,得證幾何報酬率同樣會收斂至µ - 1/2 * σ^2。

條條道路通羅馬 ?

四、多資產投組矩陣算法
前面的推導知道了幾何報酬率的近似公式,接下來要進一步到投資組合的階段。
考慮一個投組權重w、個股算術報酬率µ、個股共變異數矩陣Σ。
投組的算術報酬率以及變異數可寫作下式。
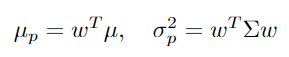
接下來將G對投組權重w微分就是最佳權重。

------------------------------以下開始實證-------------------------------
實證設定:
標的:S&P 500 Total Return Index、TLT(20年以上公債)、GLD(黃金)
資料來源 : Yahoo Finance
資料起始:1988-01-04 S&P 500 , 2002-07-30 TLT , 2004-11-18 GLD.
一、單資產最佳槓桿率
- 測試單資產不設算利率,起始日均為各個資產有報酬的第一天。

黃色底是根據公式所計算出來的最佳槓桿率,紅色字是最佳淨值。
雖然仍有些許誤差,但最大淨值的槓桿率已經相當接近最佳槓桿率。
槓桿3.79倍 S&P 500 可以達到驚人的"4033"倍。
- 設算日利率為3%除以252,平均分散在各個交易日。

S&P 500 最終成長的淨值從 4033 降至 115 倍,不過先不要太失望。
二、多資產最佳槓桿率
- 測試多資產不設算利率,起始日為GLD上市後(2004-11-18)。

上圖比較了最佳槓桿多資產投組、最佳槓桿(3.17倍) S&P 500 以及沒有槓桿的S&P 500。
同時期這三種策略各自成長了5232.24、36.87、7.02倍。
最佳投組做多3.9倍S&P 500、3.42倍TLT以及2.54倍的GLD,這就是透過資產配置減小波動耗損並增加槓桿的威力。
- 設算日利率為3%除以252,平均分散在各個交易日。

添上了利息後,多資產投組又贏了。三種策略各自成長了49.29、7.45、3.88倍,單壓股票的最佳槓桿率降至2.36倍。
最佳投組做多2.68倍S&P 500、1.65倍TLT以及1.9倍的GLD,這顯示單壓股票不是最好的選項,事實上,有許多方式可以證明大多數情形單壓股票的長期報酬不會比多資產槓桿來的優。
不信?
三、限制槓桿上限之多資產最佳槓桿率
上面的最佳投組總槓桿率是6.23倍,明顯超過2.36倍的S&P 500最佳槓桿率。為了「公平起見」,這次我們利用數值解的方式求取限制槓桿上限的多資產最佳槓桿率。

Still the same. 多資產投組贏麻了
在槓桿倍率2.36倍的情形下,配置1.33倍的S&P 500以及1.03倍的GLD能夠達到最大的報酬,超越了2.36倍的S&P 500。毫無疑問地,最大回撤也如預期下降許多。
有趣的是在限制2.82倍槓桿時,就會需要開始做多TLT,這對於理解多資產槓桿為何有效至關重要,每個資產壓到一定的程度,經常就需要找其他長期上漲的資產進行分散。
結語
本篇文章的前半段提供了四種方式計算最佳槓桿率,其中我最喜歡幾何布朗運動以及矩陣算法,後半段實證了公式與回測績效相當地接近,其誤差是幾乎可以被忽略。
後半段的實證是投資人最在乎的,搞了一堆數學究竟對投資有什麼幫助?我們得知多資產槓桿投組在大多數情形下不僅總報酬會贏過單資產,而且最大跌幅還會更小。這是因為槓桿增加會使波動耗損急遽上升,當某個資產壓了很大的比重,多資產槓桿投組就會開始轉買低相關性且權重較低的資產,減緩波動耗損帶來的負面影響。有興趣的話可以透過檢驗幾何報酬對單一資產偏微分得到這個結論。
在文章一開始時有提到
我們得出一個簡單的結論是:「市場平盤的狀況,小於一倍的槓桿可以得到波動利益,大於一倍的槓桿反而會得到波動耗損。」這個結論相當重要,理解這個結論後就可以間接地理解為什麼多資產槓桿經常會比單資產槓桿還要來得更好。
為什麼這個結論很重要?波動上升的狀況下,如果兩個資產零相關,50%/50%的多資產投組會因此獲得許多波動利益。即便你開了槓桿,100%/100%在數學上也不會有波動利益/耗損。更特別的是,如果兩個資產負相關,100%/100%投組在波動上升時期甚至可以得到波動利益。所以債券、黃金對投資組合報酬的影響,絕對不能單看債券、黃金的個別走勢就定論,而是需要嚴謹的計算投組內各個資產的波動、相關性,才可以得到理性且科學的結論。
最後,最佳槓桿率僅有事後才能觀測的到,我們不知道未來股票最佳槓桿率是0.5倍還是3倍,也不知道未來什麼樣的股債比例是最好的,但可以確定的是如果要上大槓桿,分散總是會有好處。除此之外,我也認同半凱利的想法,壓在最佳槓桿率是非常危險的一件事情,壓凱利公式的一半是稍微合理一點的方式。
文章若有任何寫錯的地方,歡迎留言指證或聯絡
FB : Jin 槓桿指投Lab
參考資料:























