編輯嚴選

[探索] 門外漢的梯度下降變奏曲（下）

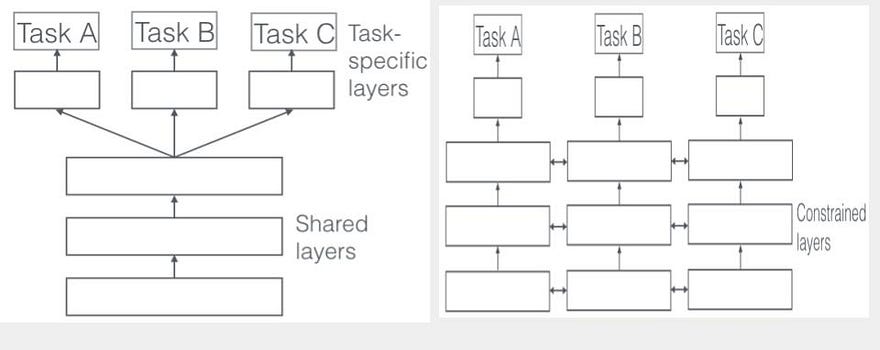
在（中）一文中，我們瞭解如何使用指數衰退移動平均來達到動態調整後，接著我們來仔細看看如何對參數更新方法所做的變化處理來改善梯度下降法。在這個類別下，主要會提及利用指數衰退係數來實現動量學習法。

動量這個詞在遵循牛頓定理的剛體運動是極活躍的使用，指的是物體在運行時所具有的能量，用數學式表達即是質量乘上速度。而在最佳化的領域，我們可以把最佳化演算法當成在損失函式曲面行進單位重量為一的球。這顆由最佳化演算法偽裝的球，除了計算當下該點的梯度當作參數更新的步進量外，更仰賴過去運動慣性所維持的速率來制衡梯度變化造成的震盪，加速前進。而根據動量變化而得到的速度變化，則可以看作對學習率的調整。

至於動量的實現上完成了什麼，我們可以從在（上）所提到的局部最小值講起。局部最小值，包括使最佳演算法停滯不前的平坦區域和鞍點周遭的緩坡，將動量加入學習演算法，有助於克服這些局部最小點的問題。事實上，動量解決了兩個問題，除了在平坦區域中常見隨機梯度變異數（variance of stochastic gradient）外，就是病態二階導數矩陣。隨機梯度變異數就是在學習的過程中出現震盪的問題，有時是學習率值過大造成，有時則是演算法本身使用隨機取樣的方法來估算梯度，如隨機梯度下降法。而病態二階導數矩陣，所造成的橢圓體曲面（如下圖所示），則會在長軸高曲度的地方運行時產生震盪。

若初始在橢圓體曲面的長軸，則依據梯度下降法，隨著最陡梯度的方向前進。然而，若學習率設的太大時，最陡梯度的方向恰巧會沿著長軸來回震盪。在不改變學習率，該如何使用動量達成減小震盪呢？這裡我們希望能夠藉著過去動量提供的速度前進，而非跟隨著梯度的方向，就如紅色軌跡所示，在長軸路徑上的每一點速度緩降下來，相當於縮小學習率 ，以免產生大幅度震盪。

圖片來源：DeepLearning book Ch 8

動量方法可以減小震盪的原因，在於它不如標準隨機下降法，直接使用該點的梯度來更新參數。相對地，它會使用一個叫做速率的變數，該變數會同時考慮並累積過去幾個迭代的梯度變化，和包含該點所計算出的梯度變化量，當然，如同標準隨機下降法所做的，給梯度變化一個負值。值得一提的是，隨著迭代數目的增加，餃古遠的速率值會很合理的逐漸被淡忘，失去它對當下最佳化方向的影像力。

在實現此步驟，數學上則是使用先前介紹的指數衰退加權方法，而在可調參數（hyper-parameter）的個數上，則是多了一個動量指數衰退係數。這個動量指數衰退係數必須要介於一和零之間，以保證在迭代的過程中，較古遠的梯度歷史會被遺忘。這裡提供調整動量指數衰退係數的簡單準則：若動量指數衰退係數接近零，則能記憶的歷史變得很少，所以最佳化演算法的表現上則是比較仰賴當次迭代所計算出的梯度，也就是靠近標準隨機梯度下降法的行為。當動量指數衰退係數接近一，最佳化演算法表現上則高度被過往梯度歷史所影響，不易產生震盪，但不容易對當前的梯度變化產生反應，而呈現緩慢變化的現象。

在這裡，讀者可能想問，有沒有一個方法可以使用一個較大的動量指數衰退係數，而不受過去羈絆呢？答案是可以的，而魔術就在 Nesterov 動量。

Nesterov 動量法是動量方法的變形。該方法和標準動量法的不同處於在哪一點取偏微。Nesterov 動量法會使用 一種稱為 Nesterov 加速度梯度的方法（Nesterov’s accelerated gradient）來進行梯度的運算。如前所述，該演算法在取梯度時，不會像標準動量方法（下圖藍色向量）使用該迭代的參數值，然而是先「往前看」（look ahead），意為除了當次迭代之參數值又加上了已加權過的速度變數（下圖棕色向量）作為「往前看」參數位置。而梯度的計算（下圖紅色向量），就是在「往前看」位置來計算，如圖下方：

這樣做的合理性在於，反正在參數更新的時候，都會更新已加權過的速度變數，所以先取參數的「往前看」位置，偷看這裡的梯度變化如何，並預先做準備。而由於 Nesterov 動量法「往前看」的做法，比起標準的動量方法，在動量指數衰退係數大的情況下，更能快速反應梯度的大幅度變化。這是因為利用「往前看」位置所計算的梯度會比「現在」的梯度為大，而能夠減少動量的累積，因此更快反應。另一方面，Nesterov 動量法比起標準動量法會擁有較小震盪，尤其在曲度較大的區域。 但整體而言，比起標準動量法，使用 Nesterov 動量法並沒有較快的收斂率。

雖然加入動量可以造成如動態改變學習率的效果，然而在非常高維的參數空間，使用動量來調節是遠遠不夠的。所以最佳化的專家們在 RMSprop 發表之後，突然靈光一閃，何不如結合動量和動態更改學習率的方法，創造一個新的演算法呢？數學家們拍手附和，因為在 RMSprop就已經使用移動平均的方式來計算梯度的第二統計動差，也就是未減去平均值的梯度變異。而動量計算正好可視為第一統計動差也是梯度平均值，於是上帝就給了我們亞當（Adam）。

Adam 的作者們希望能應用指數衰退加權移動平均到梯度的估算上，所以他們將動量和未減去平均值的梯度變異分別用兩個變數獨立計算，最後再用動量當作該次需要更新的梯度量，用未減去平均值的梯度變異變數的方根倒數來做學習率動態調整。使用指數衰退權重的方法來計算動量，和標準動量法的不同處在於如何處理當次迭代的梯度。標準動量法認為當次迭代的梯度和過去梯度歷史是獨立的變數，加大過去梯度歷史的指數衰退係數並不會抑制當次迭代的梯度量。然而，對於 Adam 而言，若增加指數衰退加權係數會抑制當次迭代的梯度量，所以又有人稱呼 Adam 方法宛如一個在損失曲面坡道運行，但同時受到坡道阻擋的球，又被稱為 Heavy Ball with Friction (HBF) 「註一」。

在發展梯度下降演算法變異時，可以發現一個大致趨勢，就是利用指數衰退移動平均來計算梯度的第一或第二統計動差。然而過於天真的使用指數權重移動平均會有一個問題，那就是演算法一開始初始為零的移動平均值。而這個簡易的初始方法帶給計算結果的影響是移動平均值的初始估計會較原來的數值分佈偏低，而造成偏移的問題。所以，為了能夠得到準確的估算，必須做偏差校正（bias correction）。

校正的方法主要是除上（1 - 指數衰退權重的 k 次指數），這裡的 k 代表的是迭代的數目。這樣的誤差調整有一個特質，那就是當迭代數目變大時，包含偏移校正的值會等同於原來指數衰退權重移動平均的公式。讀者可以參考下圖了解指數加權平均和有無偏差校正的影響。

為了能夠更準確捕捉損失函示的局部梯度變化趨勢，Adam 在估算移動時還做了偏差校正。為了能夠不靜止於局部最小區域，Adam 運作有如一顆重球在具有摩擦力的平面運行，能夠跳越局部陡峭的最小值（受當次迭代梯度影響）而到達泛化能力就好的平坦區域最小值。

雖然 Adam 看起來美好，但他也有一些問題並衍生了一些兒子兒孫，我們現在就來看看這些 Adam 兒孫解決什麼問題。

Adam 在 ICLR 2015 會議中初登場後，受到使用類神經網路的學者們喜愛，幾乎成為許多研究領域的最愛預設最佳化演算法。然而，Adam 未能經過時間的考驗，在隨後一些研究指出 Adam 在某些情況表現不如使用單純的隨機下降法加上動量，尤其是在泛化能力上， Adam 無法如當初所想可以廣泛應用在不同的任務中「註二」。

針對 Adam 種種的不是，最佳化演算法得專家們已經演化了各有特色的 Adam 子孫們，包括了：

與 Adam 由同一作者們在同一篇論文（見參考資料 [2]）同時發表的 AdaMax ，主要是替換動態調整學習率的梯度第二動量估計值，從取 l2 範式項改為在過去梯度和當次梯度中取最大值。在這個替換中，無需做偏移校正。雖然不如取 l2 範式項具有連續性，但也能穩定收斂到一個最小值。

NAdam （Nesterov-accelerated Adaptive Moment Estimation）引入 Neterov 動量中「向前看」位置來計算當次迭代的梯度，變更了更新的公式以包含這項改變。

AdamW 則解決了包涵 weight decay 大部分的實作問題。

連同上兩篇文章，我們介紹了機械學習裡的基石，並踩著這些基石了解了改變資料餵送方式，以及動態改變學習率或在更新項中加入動量的方法。我們可以看到這些梯度下降的變化，主要是解決兩個問題：梯度震盪和非最佳的局部最小值造成學習停滯不前的問題。

然而這些技巧僅僅只是冰山的一角，接著我們將會把梯度下降法放進類神經網路的脈絡中。我們會提到正向傳播，和它的雙胞胎兄弟，反向傳播，在較為一般的網路架構，如 Feedforward 類神經網路。在對處理影像而特化的卷積網路，以及對序列資料特化的 Recurrent network。

這意味著，我們將要在未來的文章中，討論 dropout [註三] ， batch normalization 和 ReLU activation function，這些專注於類神經網路的技巧。

[註一] 關於 Heavy Ball with Friction (HBF) 可以參見 GANs Trained by a Two Time-Scale Update Rule：Converge to a Local Nash Equilibrium 這篇論文。在文章中，作者使用兩個不同衰退速率分別來最佳化生成者（generator）損失與仲裁者（discriminator）損失。同時，在他們的研究中，也發現 Adam 運作方式有如一顆重球在具有摩擦力的坡面前進。

[註二] 關於 SGD + Momentum 方法勝於 Adam 可見 Improving Generalization Performance by Switching from Adam to SGD 論文。此篇的作者發現與其單一的使用 Adam，他們發展一種稱為 SWATS 的演算法排程方法。在一開始使用 Adam，過一段時間當最佳化歷程符合某些條件後，轉為 SGD + Momentum。而另一篇文章 The Marginal Value of Adaptive Gradient Methods in Machine Learning 則是歸類 Adam 在 Adaptive Learning Rate 的方法中（如 Adagrad 和 RMSprop），並發現此類方法演算法都有不易泛化問題。

[註三] 在 Rashmi Korlakai Vinayak 和 Ran Gilad-Bachrach 的努力下，將 dropout 應用在 Boost Tree。請參考論文 DART: Dropouts meet Multiple Additive Regression Trees