互動遊戲題 最後一隻螞蟻落下的時間. Last Moment All Ants Fall_Leetcode 1503

這題的題目在這裡:

題目敘述

題目會給我們兩個陣列left, right 分別代表每隻螞蟻所在的初始位置 和 方向，n代表木板長度。每隻螞蟻每秒鐘前進一單位長度。

問我們，每隻螞蟻從初始位置出發，0秒起算，當兩隻螞蟻相遇時，會互相掉頭，往相反方向前進，問最後一隻螞蟻掉落木板的時候是幾秒鐘?

測試範例

Example 1:

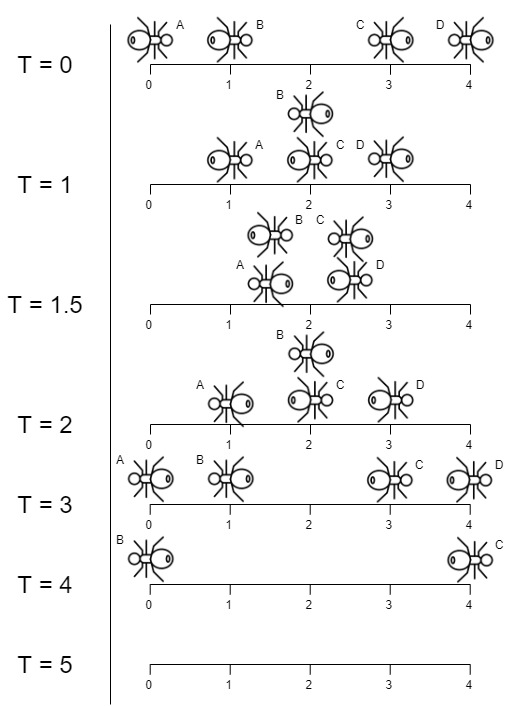
Input: n = 4, left = [4,3], right = [0,1]
Output: 4
Explanation: In the image above:
-The ant at index 0 is named A and going to the right.
-The ant at index 1 is named B and going to the right.
-The ant at index 3 is named C and going to the left.
-The ant at index 4 is named D and going to the left.
The last moment when an ant was on the plank is t = 4 seconds. After that, it falls immediately out of the plank. (i.e., We can say that at t = 4.0000000001, there are no ants on the plank).

Example 2:

Input: n = 7, left = [], right = [0,1,2,3,4,5,6,7]
Output: 7
Explanation: All ants are going to the right, the ant at index 0 needs 7 seconds to fall.

Example 3:

Input: n = 7, left = [0,1,2,3,4,5,6,7], right = []
Output: 7
Explanation: All ants are going to the left, the ant at index 7 needs 7 seconds to fall.

約束條件

Constraints:

• 1 <= n <= 104
• 0 <= left.length <= n + 1
• 0 <= left[i] <= n
• 0 <= right.length <= n + 1
• 0 <= right[i] <= n
• 1 <= left.length + right.length <= n + 1
• All values of left and right are unique, and each value can appear only in one of the two arrays.

演算法

這題其實算是個腦筋急轉彎的題目，若是用模擬交換方向的演算法，可能會很複雜。

關鍵在於，兩隻螞蟻相遇時，交換方向 和 不交換方向其實是等價的，並不影響最終結果。

以這個例子來說，初始方向 A 往右走，B往左走

A 往右走，B往左走
-----> A B <--

After A, B meet each other
相遇之後，AB交換方向​

<----- A B -->

Max(5, 2) = 5
最後一隻(左邊那隻)在5秒鐘的時候掉落 
​
is equivalent to 
相遇之後，AB不交換方向​ 其實也是等價的

<----- B A -->

Max(2, 5) = 5
最後一隻(左邊那隻)在5秒鐘的時候掉落

推廣到更多隻螞蟻相遇，也是同樣等價的結果。

所以，掌握這個關鍵之後，一切都變得簡單許多。

讓每隻螞蟻依照初始方向，從給定的位置一直往前走，每一秒往前走一單位長度。
相遇也不交換方向(因為在這題的條件下，不交換 和 交換是等價的)，一直走到最後一隻螞蟻掉落木板為止。

我們只要計算每隻螞蟻距離木板兩端點的最大值，最後再取一次最大值，就是最後一隻螞蟻掉落木板的秒數，也就是題目所求的最終答案。

程式碼

class Solution:
　def getLastMoment(self, n: int, left: List[int], right: List[int]) -> int:

　　# Ants keep going is equivalent to ants exchange direction

　　# Max time to left endpoint for ants going to left hand side
　　time_to_left = max( left or [0] )

　　# Max time to right endpoint for ants going to right hand side
　　time_to_right = max( [ n - position for position in right] or [0] )

　　return max(time_to_left, time_to_right)

複雜度分析

時間複雜度: O( n)
兩次線性掃描，最大長度和木板長度一樣長O(n)。

空間複雜度: O(n)
兩次線性掃描，臨時陣列的最大長度和木板長度一樣長O(n)。

關鍵知識點

關鍵在於，兩隻螞蟻相遇時，交換方向 和 不交換方向其實是等價的，並不影響最終結果。(建議在紙上畫個圖，加深印象，這題算是滿經典的腦筋急轉彎題目。)

Reference:

[1] Python O(n) just keep going and get maximal distance. [w/ Comment] - Last Moment Before All Ants Fall Out of a Plank - LeetCode